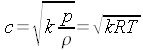
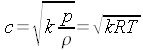
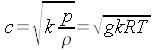
 Si definisce numero
di Mach (M) il rapporto (adimensionale) tra la velocità del fluido
e la velocità locale del suono:
Si definisce numero
di Mach (M) il rapporto (adimensionale) tra la velocità del fluido
e la velocità locale del suono:| Simulazione Effetto Doppler |
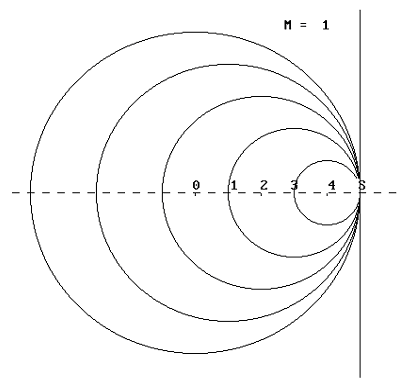 Nel caso che la
velocità della sorgente sia uguale a quella del suono, la sorgente si sposta rimanendo
sempre sul fronte d'onda; tutti i fronti d'onda di perturbazioni emesse successivamente,
saranno tutti tangenti fra di loro nello stesso punto. Il piano tangente alle
sfere in questo punto viene chiamato piano di Mach; esso divide lo spazio in due
parti. La parte dello spazio non raggiunta dalla perturbazione si chiama zona
del silenzio.
Nel caso che la
velocità della sorgente sia uguale a quella del suono, la sorgente si sposta rimanendo
sempre sul fronte d'onda; tutti i fronti d'onda di perturbazioni emesse successivamente,
saranno tutti tangenti fra di loro nello stesso punto. Il piano tangente alle
sfere in questo punto viene chiamato piano di Mach; esso divide lo spazio in due
parti. La parte dello spazio non raggiunta dalla perturbazione si chiama zona
del silenzio.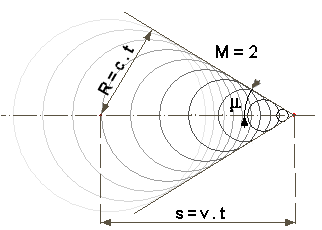 Nel caso che la sorgente sia ferma e il
mezzo si muova alla velocità del suono, il piano di Mach è fisso e la zona del
silenzio indica la zona che non verrà mai raggiunta dalla perturbazione.
Nel caso che la sorgente sia ferma e il
mezzo si muova alla velocità del suono, il piano di Mach è fisso e la zona del
silenzio indica la zona che non verrà mai raggiunta dalla perturbazione.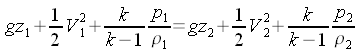
| A suo tempo, parlando di trasformazioni isentropiche è stato trovato il lavoro compiuto durante la trasformazione; che fine ha fatto questo lavoro se abbiamo detto che nell'ipotesi di validità dell'equazione di Bernoulli non viene compiuto lavoro sull'esterno? |
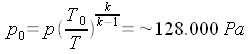
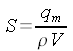
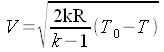
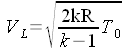
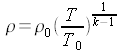
| Deflusso da un serbatoio |
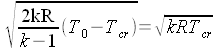
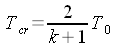
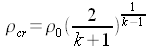
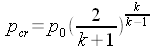
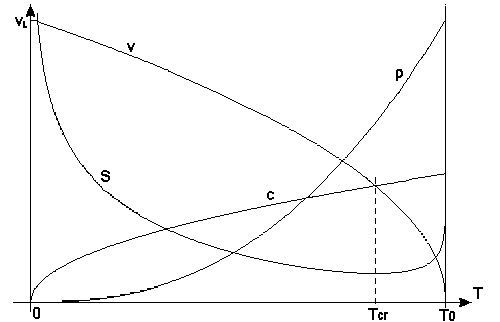
| Breve riepilogo: per poter raggiungere velocità supersoniche
un gas si deve espandere fino ad una pressione inferiore a quella critica. Inizialmente
la sezione del tubo di flusso diminuisce all'aumentare della velocità (come
succede anche per i liquidi); ma, dopo che è stata raggiunta la pressione
critica avviene tutto il contrario, cioè all'aumentare della velocità
aumenta anche la sezione del tubo di flusso. Per spiegare questo 'singolare' comportamento pensiamo al fatto che, in regime supersonico, la densità diminuisce più rapidamente di quanto aumenti la velocità. Lo stesso discorso vale all'inverso: un fluido supersonico per diventare subsonico (in modo graduale) deve passare attraverso la sezione critica. Una sezione ristretta per poter essere una sezione critica deve permettere il raggiungimento dei parametri critici: in caso contrario il fluido non cambia le proprie caratteristiche (se era supersonico rimane supersonico). |
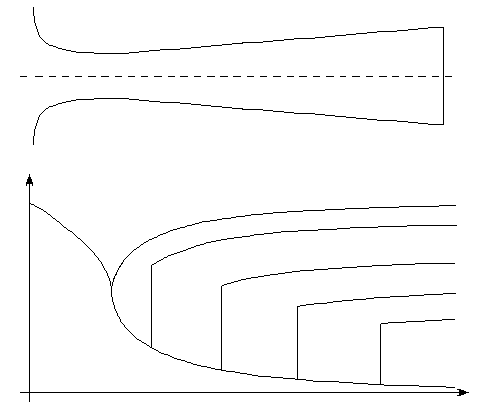
Affinché si possa raggiungere una velocità supersonica (e quindi
con espansione sempre isentropica), il flusso deve essere guidato; è
necessario, cioè, un condotto convergente-divergente chiamato tubo
di De Laval.
Nella figura che segue è riportato l'andamento della pressione, densità
e temperatura lungo il tubo di De Laval.
| Problema: Calcolare
le dimensioni di massima di un tubo di De Laval che, applicato ad un serbatoio
ove vi è una pressione di 3000 hPa, temperatura 800 K, permetta l'espansione
di 5 kg/s di aria fino alla pressione esterna di 1000 hPa. Calcoliamo la densità nel serbatoio: (equazione di stato). 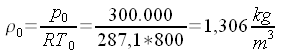 Calcoliamo le condizioni critiche: 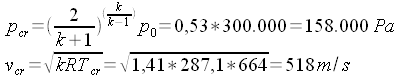 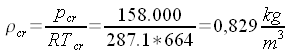 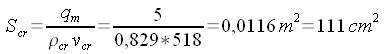 Calcoliamo la sezione di uscita: (eq. di stato) (eq. di Bernoulli) (eq. di continuità) 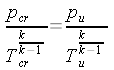 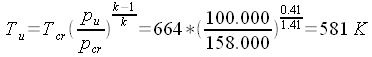 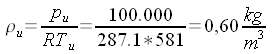 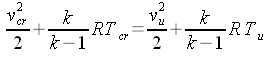 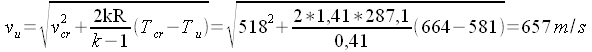 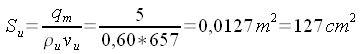 A questo punto, note le dimensioni di massima, ed imponendo che il divergente abbia un'apertura non superiore a 7° - 8° (per evitare il distacco dello strato limite), e raccordando opportunamente il convergente con la sezione critica non è difficile disegnare il tubo. |
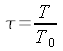
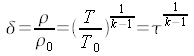
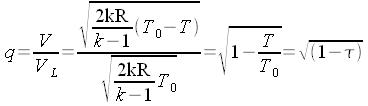
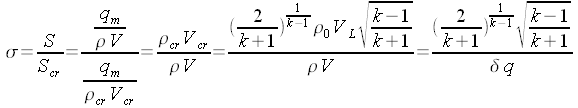
essendo:
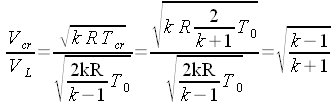
Infine:
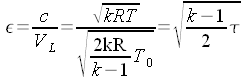
Per questo programma, il cui listato è riportato in appendice, è
stato utilizzato il Java. In esso viene creata un tabella in cui sono riportati
i valori calcolati) che potranno essere copiati e incollati in altre applicazioni;
contemporaneamente tutti questi valori sono riportati su un grafico (la sezione
in scala logaritmica).
L'output di questo programma è riportato nel grafico e nella tabella
che seguono.
Spinta fornita dal tubo di De Laval
La funzione del tubo di De Laval è, ovviamente, quella di lanciare il
gas a velocità supersoniche.
Contemporaneamente su di esso si crea, per reazione, una spinta che può
essere facilmente calcolata applicando il teorema della quantità di moto:
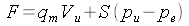
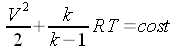
Osservazione: l'equazione di Bernoulli perde di validità quando la si applica fra due sezioni che contengono l'onda d'urto; si può, invece, continuare ad applicarla quando le due sezioni sono entrambe a monte o entrambe a valle dell'onda d'urto. La trasformazione adiabatica (non ideale) che subisce il fluido non appartiene nemmeno alla famiglia delle politropiche; l'espressione che la rappresenta è chiamata equazione di Rankine-Hugoniot. Per il calcolo della velocità critica si può prendere in considerazione sia la sezione di ristagno a monte che quella a valle (anche se potrebbe non aversi alcun ristagno nel fluido), dato che la temperatura di ristagno a monte e a valle sono uguali; per rendersene conto, applicare l'equazione dell'energia fra due ipotetiche sezioni di ristagno a monte e a valle dell'onda d'urto. |
| Problema: In corrispondenza del bordo di attacco della fusoliera,
quando la corrente è supersonica, si forma un'onda d'urto staccata. Per la linea
di corrente che subisce l'arresto tale onda può considerarsi normale. Sia: V1 = 500 m/s, p1 = 1000 hPa, ρ1 = 1,225 kg/m3, T1 = 288 K. Ricavare le corrispondenti grandezze a valle dell'urto, per il filetto fluido che subisce l'arresto, e i valori di ristagno a monte e a valle dell'urto. Troviamo le grandezze di ristagno a monte dell'urto. Dall'equazione di Bernoulli: Dall'equazione della trasformazione: 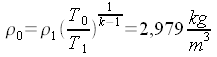 Dall'equazione di stato: La velocità critica al quadrato è: 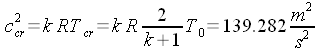 Dalla relazione di Prandt: 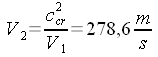 Applichiamo, infine, l'equazione di continuità: 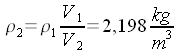 l'equazione della quantità di moto: e l'equazione di stato: 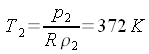 Da notare che, avendo usato l'equazione di stato per trovare la temperatura, non abbiamo usato l'equazione dell'energia. Calcoliamo ora le grandezze di ristagno a valle dell'urto. Dall'equazione di Bernoulli: Dall'equazione della trasformazione: 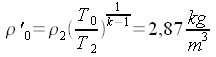 E, infine, dall'equazione di stato: Confrontiamo i risultati per mettere in evidenza una cosa generale: T0 = T0' , p0 > p0' , ρ0 > ρ0'. |
 Prendiamo in considerazione
un profilo alare immerso in una corrente subsonica. Sappiamo che, in questo caso,
il fluido subisce prima un rallentamento; si ferma in prossimità della bordo di
attacco; poi la sua velocità torna ad aumentare, raggiunge il massimo in prossimità
del massimo spessore del profilo e poi torna a diminuire. Il tubo di flusso presenta
quindi un tratto convergente, una sezione ristretta e poi un tratto divergente.
Prendiamo in considerazione
un profilo alare immerso in una corrente subsonica. Sappiamo che, in questo caso,
il fluido subisce prima un rallentamento; si ferma in prossimità della bordo di
attacco; poi la sua velocità torna ad aumentare, raggiunge il massimo in prossimità
del massimo spessore del profilo e poi torna a diminuire. Il tubo di flusso presenta
quindi un tratto convergente, una sezione ristretta e poi un tratto divergente.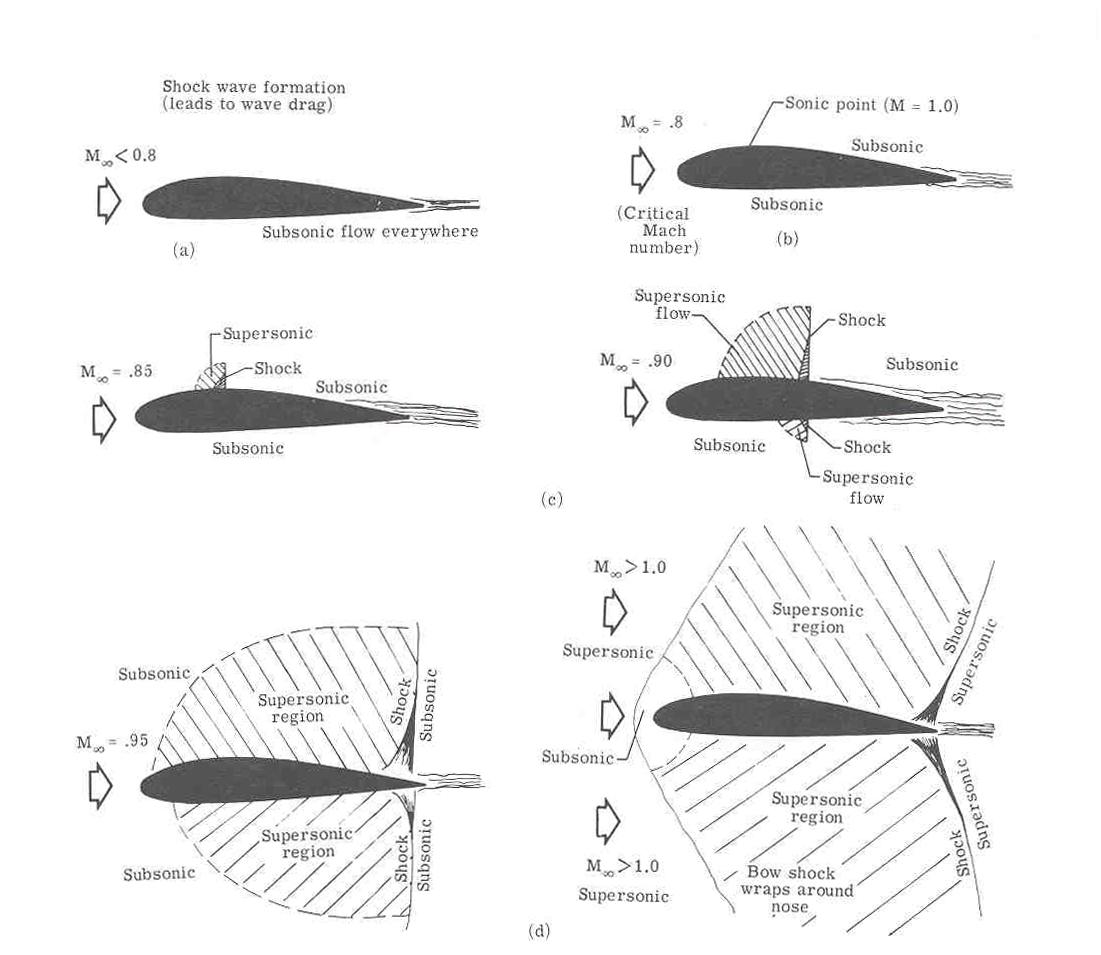 A
velocità maggiori l'onda d'urto, sempre più arretrata, si inclina
sempre di più e diventa sempre meno forte. A velocità grandi l'onda
d'urto, per quanto produca un aumento di pressione, è debole e la velocità
del fluido rimane supersonica; per cui, all'aumentare della sezione del tubo di
flusso la velocità del fluido continua ad aumentare e la sua pressione
continua a diminuire. Si rende necessaria un'altra onda d'urto che avviene in
prossimità del bordo d'uscita.
A
velocità maggiori l'onda d'urto, sempre più arretrata, si inclina
sempre di più e diventa sempre meno forte. A velocità grandi l'onda
d'urto, per quanto produca un aumento di pressione, è debole e la velocità
del fluido rimane supersonica; per cui, all'aumentare della sezione del tubo di
flusso la velocità del fluido continua ad aumentare e la sua pressione
continua a diminuire. Si rende necessaria un'altra onda d'urto che avviene in
prossimità del bordo d'uscita. All'aumentare della
velocità l'onda d'urto si avvicina sempre di più al bordo di attacco
dell'ala e la zona in cui il deflusso è subsonico diventa sempre più
piccola, facendo così diminuire la resistenza d'onda.
All'aumentare della
velocità l'onda d'urto si avvicina sempre di più al bordo di attacco
dell'ala e la zona in cui il deflusso è subsonico diventa sempre più
piccola, facendo così diminuire la resistenza d'onda.