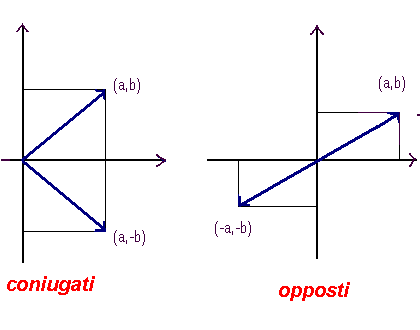Sappiamo già che i numeri reali si possono porre in corrispondenza biunivoca con i punti della retta.
E' ugualmente possibile dare un'immagine geometrica ai numeri complessi? Fu GAUSS a dare piena dignità ai numeri complessi mediante la loro
rappresentazione su un piano, detto appunto il piano di GAUSS.
Fissiamo su un piano un sistema di assi cartesiani. Il numero complesso a+ib è caratterizzato dalla coppia di numeri reali (a,b).
Sia P il punto del piano di ascissa a e di ordinata b, ebbene conveniamo di rappresentare il numero complesso a+ib con il punto P. Il punto P costituisce
l'immagine geometrica del numero complesso dato e, viceversa, ad ogni punto del piano corrisponde un numero complesso avente per parte reale l'ascissa del punto P
e per coefficiente della parte immaginaria l'ordinata del punto P.
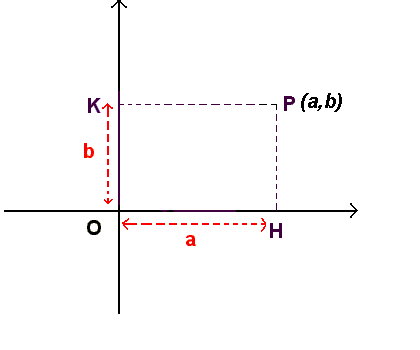Abbiamo visto che al numero complesso a+i b possiamo associare il punto P del piano di Gauss di coordinate (a,b), ma il punto P individua anche il vettore OP, quindi possiamo dire che al numero complesso a+ib corrisponde il vettore avente a come
sua componente secondo l'asse x e b come componente secondo l'asse y.
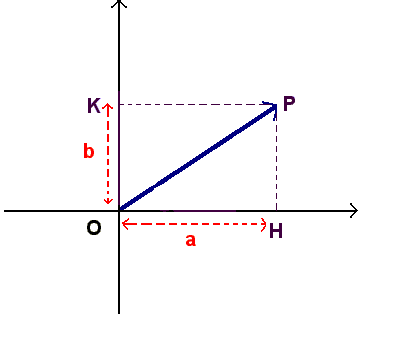Nel piano di Gauss numeri complessi opposti sono rappresentati da due vettori opposti, mentre due numeri complessi coniugati sono rappresentati da due vettori simmetrici rispetto all'asse reale.
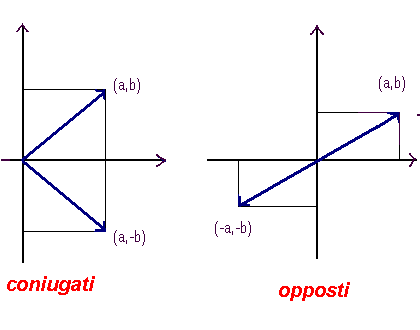
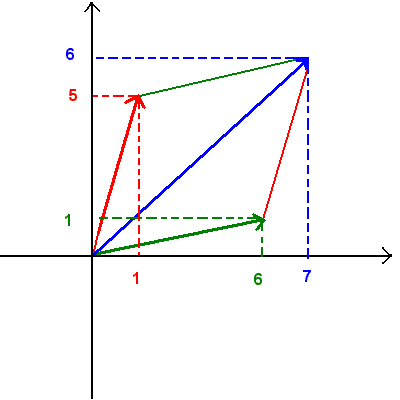
Nella figura che segue si può osservare come valga la regola del parallelogramma per la somma dei due numeri complessi z = 1 + 5i e w = 6 + i
z + w = 7 + 6i
La rappresentazione geometrica dei numeri complessi ci offre l'occasione di riflettere sul fatto che, a differenza dei numeri reali, i numeri complessi non costituiscono un insieme ordinato.
Non ha cioè senso chiedersi se, ad esempio 2+4i è maggiore o minore di -5+2i. Fra i punti del piano, infatti, non è possibile avere le analoghe relazioni di "precedere" e di "seguire" che è invece possibile introdurre sulla retta.
