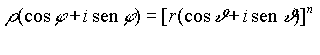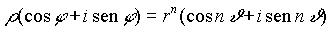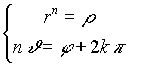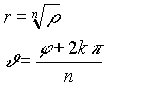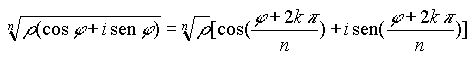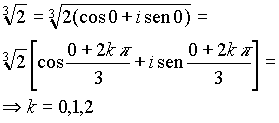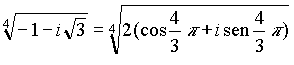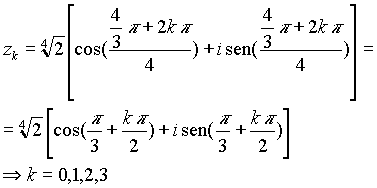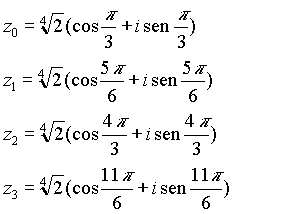RADICE n^ma DI UN NUMERO COMPLESSO

Dato un numero complesso z, in forma trigonometrica:

vogliamo trovare tutti i numeri w:

che siano le radici n^me di z. Per definizione deve risultare z = wⁿ:


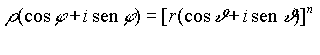
Applicando al secondo membro la formula di DE MOIVRE, avremo:


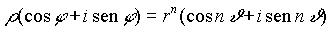
Perchè quest'uguaglianza sia soddisfatta dovrà risultare:


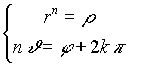
da cui segue che:

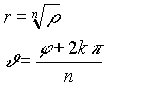
Concludendo, diremo che:

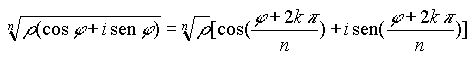
dove k può assumere gli n valori 0,1,2,.....(n-1).

Alcuni esempi:

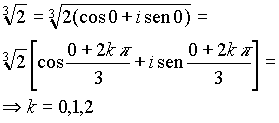
ed ecco le tre radici cubiche del numero 2:

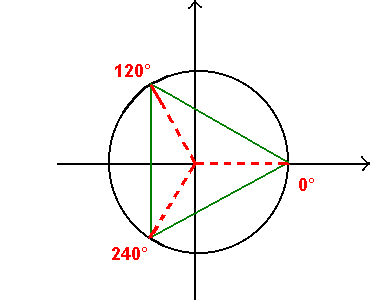
I punti, immagini delle tre radici, sono i vertici del triangolo equilatero inscritto in una circonferenza avente per raggio il modulo:

-----------------------------------


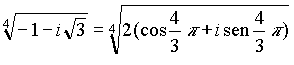
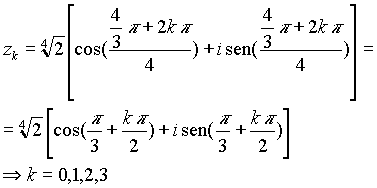
ed ecco le quattro radici distinte richieste:


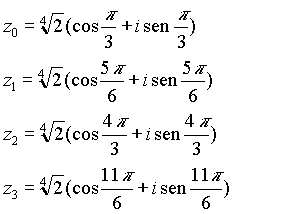
Queste quattro radici quarte hanno per immagine i vertici del quadrato inscritto nella circonferenza che ha per raggio il modulo:

Le radici n-sime di z hanno tutte lo stesso modulo (il raggio della ciconferenza) e per immagini i vertici di un poligono regolare di n lati inscritto nella suddetta circonferenza.