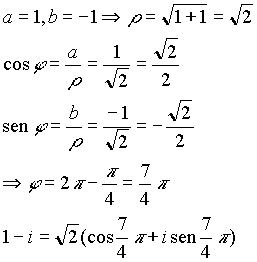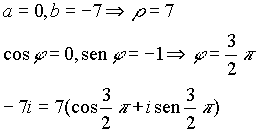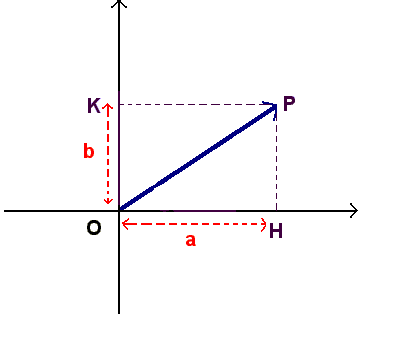
Sia OP il vettore corrispondente al numero complesso a+i b e sia r il modulo del vettore e j l'angolo che il vettore forma con la direzione positiva dell'asse x :

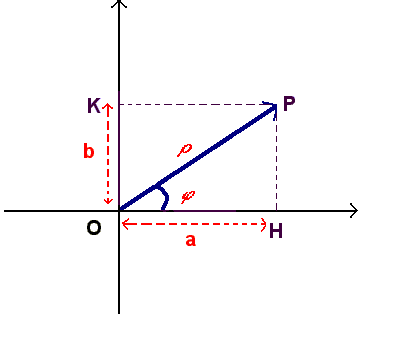
Dal triangolo rettangolo OPH si ha:

a = r cosj

b = r senj

da cui:

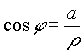
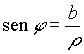
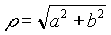
I due numeri r e j si dicono rispettivamente modulo ed argomento del numero complesso a+i b , che si potrà mettere sotto la forma trigonometrica:

a+i b = r (cosj + i senj )

r è sempre positivo, mentre l'argomento j è determinato a meno di multipli di 2p .

Due numeri complessi scritti sotto forma trigonometrica sono uguali soltanto quando hanno moduli uguali e argomenti che differiscono per multipli di 2p .

Si puņ verificare facilmente che due numeri complessi opposti hanno lo stesso modulo ed argomenti che differiscono di p ; due numeri complessi coniugati hanno lo stesso modulo ed argomenti opposti.

I numeri puramente reali hanno per argomento 0 o p a seconda che siano positivi o negativi.

I numeri puramente immaginari hanno per argomento p /2 o 3/2p a seconda che il coefficiente di i sia positivo o negativo.