La derivata
(di Maurizio Mauri)
(di Maurizio Mauri)
Data una funzione y = f(x), ricordiamo che il rapporto incrementale è definito
come:
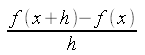
dove h è l'incremento della variabile indipendente x.
La derivata è definita come il limite del rapporto incrementale quando l'incremento h tende a zero.
Purtroppo il computer non è capace di calcolare i limiti, per cui il calcolo della derivata può farsi solo in modo approssimato. In pratica viene calcolato il rapporto incrementale con h sufficientemente piccolo. Il problema è sapere cosa vuol dire "sufficientemente piccolo" e la precisione del calcolo dipenderà molto dal valore di h stesso.
Facciamo un esempio. Supponiamo di dover calcolare la derivata della funzione y = x ex, per x = 2. Sappiamo che la derivata della funzione è ex (x + 1), che per x = 2 assume il valore 22,1671682967920.
Impostiamo un semplice programma in javascript per il calcolo del rapporto incrementale con vari valori di h. Anzitutto definiamo la funzione:
e la sua derivata (per verificare l'errore che otteniamo):
Infine costruiamo la parte del programma che calcola la derivata:
La derivata viene richiamata passando come parametro il valore
per cui bisogna dividere l'incremento al termine di ogni calcolo. Inizialmente
l'incremento è pari a 0.2. Nel nostro caso la funzione viene richiamata
con n = 2 e l'incremento viene dimezzato al termine di ogni calcolo. Questo
è il risultato del calcolo:
Come si vede l'errore è tutt'altro che trascurabile e diminuisce anche abbastanza lentamente: dimezzando l'incremento l'errore dimezza. Quest'ultimo fatto si esprime brevemente dicendo che l'approssimazione è O(h1).
Ci si potrebbe chiedere se questa è una limitazione effettiva; si potrebbe prendere un incremento piccolissimo, ad esempio 1-10, per vedere l'errore diventare accettabile. Purtroppo le cose non stanno così e per due motivi:
Si noti come, a partire dal sesto valore, l'errore invece di diminuire aumenta. Questo è dovuto proprio al fatto di utilizzare incrementi troppo piccoli.
Derivazione con punto centrale
Un importante miglioramento della precisione si ha utilizzando la seguente formula:
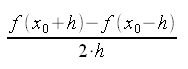
Concettualmente
non c'è niente di nuovo; la derivata viene calcolata sempre come
rapporto incrementale, addirittura con incremento doppio rispetto al precedente
metodo. La differenza consiste nel fatto che il punto in cui bisogna calcolare
la derivata si trova nel mezzo dell'intervallo e non più all'estremo
dello stesso.
Il miglioramento che si ottiene è notevole, tanto che dimezzando l'incremento, l'errore che ne risulta è un quarto del precedente e cioè è proporzionale al quadrato dell'incremento. La precisione è O(h2).
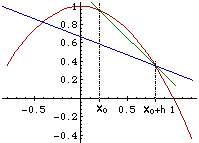
Per capire il motivo della migliorata precisione si guardi la figura che mette al confronto i due differenti metodi. La dimostrazione più rigorosa (che verrà omessa) si ha considerando lo sviluppo in serie di Taylor della funzione.
Facciamo invece il solito programmino per calcolare la derivata, questa volta prevedendo soltanto che gli incrementi dimezzino al termine di ogni calcolo:
che dà luogo ai seguenti risultati:
Si noti come l'errore diventi quattro volte più piccolo quando si dimezza l'incremento. Si noti inoltre come con h = 0.00156 (ampiezza dell'intervallo 0.0031) si ottenga un errore che con il precedente metodo si otteneva per h = 0.000001, 3000 volte più piccolo.
Estrapolazione di Richardson
Il metodo si basa sul calcolo ripetuto della seguente formula:
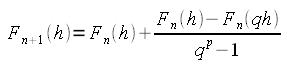A differenza degli altri metodi, per il calcolo della derivata si tiene
conto di diversi incrementi. Il fattore q nella formula (di solito pari
a 2) tiene conto degli incrementi che si ottengono moltiplicando per q
quelli precedenti.
La formula, nonostante l'apparenza, è tutt'altro che semplice e si ricava sviluppando in serie di Taylor la funzione. Noi cerchiamo di interpretarla con qualche esempio pratico.
Si parte dai valori che si sono ottenuti col il precedente metodo (con il punto al centro dell'intervallo) per due differenti incrementi h e 2h. Questi valori li indicheremo con F1(h) e F1(2h). Con questi valori possiamo ottenere un valore con approssimazione migliore della precedente, in questo caso O(h4).
Ad esempio, sono stati calcolati i valori:
F1(0.1) = 22.2287868803073
F1(0.2) = 22.4141606570294
Il valore tra perentesi rappresenta l'incremento. Da questi due valori possiamo ottenere applicando la formula precedente:
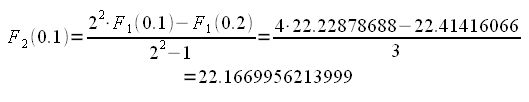con un errore pari a 0.0001726753920
Come si vede, l'errore è diminuito molto più rapidamente di quanto facesse in precedenza. Per avere lo stesso errore sarebbe stato necessario un incremento di circa 0.005.
Ovviamente il procedimento è ripetibile per ottenere un valore F3, notevolmente più preciso. Ma per far questo è necessario un altro valore di F2, quello che si ottiene con l'incremento di 0.05. Questo valore è:
F2(0.05) = 22.1671575169610
Questo valore ha un errore di 0.0000107798309, cioè 16 volte più piccolo del precedente e che mette in evidenza come la precisione sia di O(h4).
Da questi due valori si ottiene:
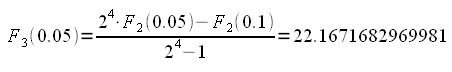con un errore di appena 0.0000000002061.
Generalizzando, scriviamo le seguenti funzioni:
La prima è il semplice calcolo della derivata con punto centrale. La seconda è invece la funzione che calcola la derivata con precisione di ordine nx. Gli altri parametri passati sono:
Ad esempio, per ottenere il fattore di ordine 4 con incremento minimo di 0.025 si richiama la funzione con rx(4, 2, 0.125, 2) e si ottiene:
Si faccia attenzione che è illusorio pensare di aumentare la precisione dei risultati diminuendo troppo l'incremento o anche aumentando il numero di iterazioni perché ci si scontra con la precisione dei calcoli effettuati dal computer. Spesso potrebbe essere conveniente richiamare più volte la funzione con diversi parametri e confrontare i risultati. Ed esempio:
Conclusione
Nel seguente modulo è possibile calcolare la derivata (con l'ultimo metodo illustrato) di qualsiasi funzione. L'unica avvertenza è che la funzione deve essere scritta secondo la sintassi javascript. Ad esempio, per la funzione:
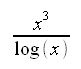si dovrà scrivere: x * x * x / Math.log(x)
Nota: per la stampa formattata viene usata la funzione printf() che non è una funzione standard del javascript; essa è contenuta in una apposita utility.
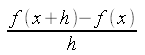
dove h è l'incremento della variabile indipendente x.
La derivata è definita come il limite del rapporto incrementale quando l'incremento h tende a zero.
Purtroppo il computer non è capace di calcolare i limiti, per cui il calcolo della derivata può farsi solo in modo approssimato. In pratica viene calcolato il rapporto incrementale con h sufficientemente piccolo. Il problema è sapere cosa vuol dire "sufficientemente piccolo" e la precisione del calcolo dipenderà molto dal valore di h stesso.
Facciamo un esempio. Supponiamo di dover calcolare la derivata della funzione y = x ex, per x = 2. Sappiamo che la derivata della funzione è ex (x + 1), che per x = 2 assume il valore 22,1671682967920.
Impostiamo un semplice programma in javascript per il calcolo del rapporto incrementale con vari valori di h. Anzitutto definiamo la funzione:
function f(x) {return x * Math.exp(x);}
e la sua derivata (per verificare l'errore che otteniamo):
function derivata(x) {return Math.exp(x) * (x + 1);}
Infine costruiamo la parte del programma che calcola la derivata:
var x = 2;
var h = 0.2;
var d;
function der(n) {var t = derivata(x);}
var nx = 0;
var h = 0.02; document.write("<table>");
printf('<tr bgcolor="#dddddd"><td align="center">Incremento<\/td><td align="center">Derivata<\/td><td align="center">Errore<\/td><\/tr>');
while (nx < 8) {d = (f(x + h) - f(x)) / h;}
printf("<tr><td> %15.10d <\/td><td> %15.13d <\/td><td> %15.13d <\/td><\/tr>", h, d, Math.abs(d - t));
h /= n;
document.write("<\/table>")
Come si vede l'errore è tutt'altro che trascurabile e diminuisce anche abbastanza lentamente: dimezzando l'incremento l'errore dimezza. Quest'ultimo fatto si esprime brevemente dicendo che l'approssimazione è O(h1).
Ci si potrebbe chiedere se questa è una limitazione effettiva; si potrebbe prendere un incremento piccolissimo, ad esempio 1-10, per vedere l'errore diventare accettabile. Purtroppo le cose non stanno così e per due motivi:
- dovendo calcolare la derivata in modo numerico spesso non abbiamo nemmeno i valori
della funzione per qualsiasi valore di x, ma solo per una serie limitata di valori
di x.
- il computer effettua i calcoli con un numero di cifre limitato, anche se
elevato. Dovendo sommare ad x un valore troppo più piccolo si ottengono
risultati senza senso ed in ogni caso errati.
Si noti come, a partire dal sesto valore, l'errore invece di diminuire aumenta. Questo è dovuto proprio al fatto di utilizzare incrementi troppo piccoli.
Derivazione con punto centrale
Un importante miglioramento della precisione si ha utilizzando la seguente formula:
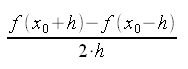
Concettualmente
non c'è niente di nuovo; la derivata viene calcolata sempre come
rapporto incrementale, addirittura con incremento doppio rispetto al precedente
metodo. La differenza consiste nel fatto che il punto in cui bisogna calcolare
la derivata si trova nel mezzo dell'intervallo e non più all'estremo
dello stesso.Il miglioramento che si ottiene è notevole, tanto che dimezzando l'incremento, l'errore che ne risulta è un quarto del precedente e cioè è proporzionale al quadrato dell'incremento. La precisione è O(h2).
Per capire il motivo della migliorata precisione si guardi la figura che mette al confronto i due differenti metodi. La dimostrazione più rigorosa (che verrà omessa) si ha considerando lo sviluppo in serie di Taylor della funzione.
Facciamo invece il solito programmino per calcolare la derivata, questa volta prevedendo soltanto che gli incrementi dimezzino al termine di ogni calcolo:
function der_cent() {var t = derivata(x);}
var nx = 0;
var h = 0.02; document.write("<table>");
printf('<tr bgcolor="#dddddd"><td align="center">Incremento<\/td><td align="center">Derivata<\/td><td align="center">Errore<\/td><\/tr>');
while (nx < 8) {d = (f(x + h) - f(x - h)) / h / 2;}
printf("<tr><td> %15.10d <\/td><td> %15.13d <\/td><td> %15.13d <\/td><\/tr>", h, d, Math.abs(d - t));
h /= 2;
document.write("<\/table>")
Si noti come l'errore diventi quattro volte più piccolo quando si dimezza l'incremento. Si noti inoltre come con h = 0.00156 (ampiezza dell'intervallo 0.0031) si ottenga un errore che con il precedente metodo si otteneva per h = 0.000001, 3000 volte più piccolo.
Estrapolazione di Richardson
Il metodo si basa sul calcolo ripetuto della seguente formula:
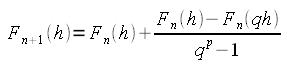
La formula, nonostante l'apparenza, è tutt'altro che semplice e si ricava sviluppando in serie di Taylor la funzione. Noi cerchiamo di interpretarla con qualche esempio pratico.
Si parte dai valori che si sono ottenuti col il precedente metodo (con il punto al centro dell'intervallo) per due differenti incrementi h e 2h. Questi valori li indicheremo con F1(h) e F1(2h). Con questi valori possiamo ottenere un valore con approssimazione migliore della precedente, in questo caso O(h4).
Ad esempio, sono stati calcolati i valori:
F1(0.1) = 22.2287868803073
F1(0.2) = 22.4141606570294
Il valore tra perentesi rappresenta l'incremento. Da questi due valori possiamo ottenere applicando la formula precedente:
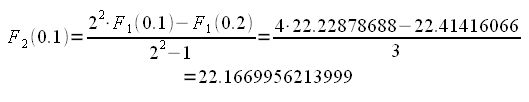
Come si vede, l'errore è diminuito molto più rapidamente di quanto facesse in precedenza. Per avere lo stesso errore sarebbe stato necessario un incremento di circa 0.005.
Ovviamente il procedimento è ripetibile per ottenere un valore F3, notevolmente più preciso. Ma per far questo è necessario un altro valore di F2, quello che si ottiene con l'incremento di 0.05. Questo valore è:
F2(0.05) = 22.1671575169610
Questo valore ha un errore di 0.0000107798309, cioè 16 volte più piccolo del precedente e che mette in evidenza come la precisione sia di O(h4).
Da questi due valori si ottiene:
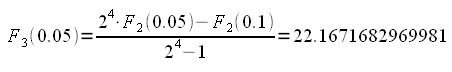
Generalizzando, scriviamo le seguenti funzioni:
function fx(h) {
return (f(x + h) - f(x - h)) / 2 / h;}
function rx(nx, x, h, p) {
var y, y1;}
if (nx < 3) {
y = fx(h);} else {
y1 = fx(h * p);
y = rx(nx - 1, x, h / p, p);}
y1 = rx(nx - 1, x, h, p);
var n = Math.pow(p, Math.pow(2, nx - 1));
return (n * y - y1) / (n - 1);
La prima è il semplice calcolo della derivata con punto centrale. La seconda è invece la funzione che calcola la derivata con precisione di ordine nx. Gli altri parametri passati sono:
- x: ascissa del punto in cui si deve calcolare la derivata;
- h: incremento;
- p: fattore per ottenere l'incremento successivo (2 in tutti gli esempi)
Ad esempio, per ottenere il fattore di ordine 4 con incremento minimo di 0.025 si richiama la funzione con rx(4, 2, 0.125, 2) e si ottiene:
Si faccia attenzione che è illusorio pensare di aumentare la precisione dei risultati diminuendo troppo l'incremento o anche aumentando il numero di iterazioni perché ci si scontra con la precisione dei calcoli effettuati dal computer. Spesso potrebbe essere conveniente richiamare più volte la funzione con diversi parametri e confrontare i risultati. Ed esempio:
Conclusione
Nel seguente modulo è possibile calcolare la derivata (con l'ultimo metodo illustrato) di qualsiasi funzione. L'unica avvertenza è che la funzione deve essere scritta secondo la sintassi javascript. Ad esempio, per la funzione:
---------------
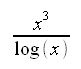
Nota: per la stampa formattata viene usata la funzione printf() che non è una funzione standard del javascript; essa è contenuta in una apposita utility.