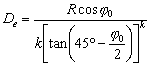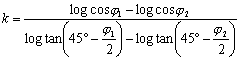| TIPO DI CARTA |
Rappresentazione analitica della superficie terrestre* |
| RETICOLO |
Meridiani: semirette uscenti dal polo P Paralleli: archi
di circonferenze concentriche di centro P |
| SISTEMA DI COORDINATE |
Polari |
| RELAZIONI DI CORRISPONDENZA: |
|
| CALCOLO DELLA COSTANTE DI CONVERGENZA: |
| con un parallelo standard |
k = sen φS |
| con due paralleli standard |
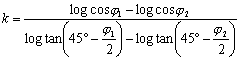 |
| se la differenza di latitudine fra i
due paralleli standard non supera i 20°,
si può porre k = sen φm |
|
| MODULO DI DEFORMAZIONE |
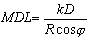 |
| PROPRIETÀ |
È conforme
Nell’ambito del foglio che si utilizza può essere considerata
equidistante (scala praticamente costante) |
| CARTEGGIO |
Nell’ambito del foglio rettifica le ortodromie
Le lossodromie sono rappresentate da curve che volgono la
concavità verso il polo
Quando si tracciano i QDM bisogna considerare la convergenza
dei meridiani |
* può essere vista come una proiezione
conica diretta modificata nella spaziatura dei paralleli per ottenere
il requisito dell’isogonismo, ma rimane essenzialmente una rappresentazione
analitica il cui reticolato è di “tipo” conico.
CARTA DI LAMBERT - Esame di Stato 2003 quesito C
Il candidato disegni una carta di Lambert isogona tangente relativa
al parallelo standard 72° N con scala, su detto parallelo, 1:20
milioni, avente come meridiano centrale quello di Greenwich. Rappresenti
ancora i paralleli 70°N e 75°N e i meridiani 30°W, 15°W, 15°E
e 30°E. Sovrapponga inoltre alla carta un reticolo il cui asse
centrale coincida con il meridiano di Greenwich e i cui pseudo-meridiani
siano intervallati di 200 NM.
Scaletta per la soluzione del quesito C/2003:
| 1. |
data la scala al parallelo di tangenza, si ricava R. |
| 2 |
dato φ0 = 72°, si calcolano k e De
. |
| 3. |
si calcolano i raggi dei paralleli richiesti (con la seconda
relazione di corr.) |
| 4. |
si calcolano gli angoli che i meridiani formano fra di
loro (con la prima rel. di corr.) e si disegna il reticolo. |
| 5. |
per l’ultima richiesta del quesito, non è specificato
a quale lat. la distanza va presa. Siccome la scala della
carta è data al parallelo di tangenza, si usa quella per
calcolare a quanto corrisponde sulla carta la distanza 200
NM, e si tracciano gli pseudo-meridiani. |
CARTA DI LAMBERT - Esame di Stato 2001 quesito D
Il candidato costruisca il reticolato relativo a una carta conica
secante isogona di Lambert con paralleli standard 52° N e
60°N limitatamente ad una regione compresa fra i paralleli
50°N e 65°N, e tra i meridiani 20°W e 20°E (paralleli
e meridiani intervallati di 5°), con scala 1/20 milioni lungo
i paralleli standard. Rappresenti inoltre sulla carta la retta
che congiunge i punti A(φ = 52°N ;λ = 15°W
) e B(φ = 62°N ; λ = 12°E ) e spieghi a cosa
corrisponde sulla sfera terrestre la detta congiungente
Scaletta per la soluzione del quesito D/2001:
| 1. |
si calcola il raggio della sfera rappresentativa sapendo
che σ1 = σ2 = Σ
= 1/(RT / R). |
| 2. |
si calcola la costante di convergenza, con la formula
esatta o con quella approssimata. |
| 3. |
si calcola il raggio dell’equatore De. |
| 4. |
con le relazioni di corrispondenza, si calcolano i raggi
dei paralleli richiesti e gli angoli che formano i meridiani. |
| 5. |
si tracciano le linee del reticolo, i meridiani e paralleli
di A e B, si uniscono A e B con un segmento. |
| 6. |
il segmento rappresenta approssimativamente un arco di
ortodromia. |
|