| ARCHI
DI MERIDIANO E PARALLELO
riepilogo
ed esercizi
Cosa devi già saper fare
- Conversioni di angoli da gradi a radianti e viceversa, da
gradi primi e secondi a gradi e decimali e viceversa.
- Conversioni di distanze nelle varie unità di misura.
- Calcolo delle funzioni coseno ed arcocoseno.
- Calcoli diretti e inversi sulle coordinate relative (Δφ
e Δλ).
- Calcoli sulla relazione spazio-tempo-velocità.
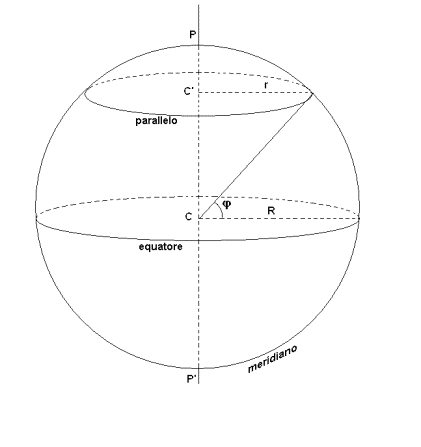
LE CIRCONFERENZE SULLA SFERA TERRESTRE
- EQUATORE: circonferenza massima => centro C e raggio R
- MERIDIANI: circonferenze massime => centro C e raggio R
- PARALLELI: circonferenze minori => centro C ’ e raggio
r
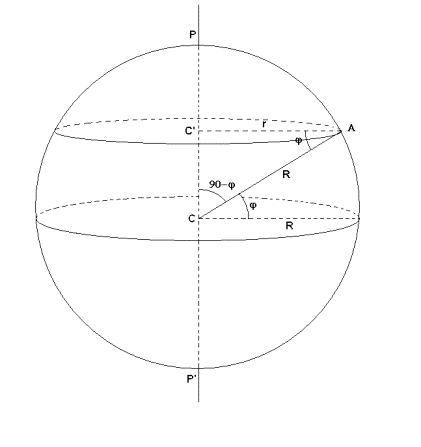
RAGGIO DEL PARALLELO
- La misura del raggio del parallelo si ricava risolvendo il
triangolo rettangolo CC’A
- A è il generico punto della superficie terrestre, di latitudine
φ
- C’ è il centro del parallelo che passa per A
- C è il centro della sfera terrestre
- L’ipotenusa AC è un raggio della sfera ed è lunga R
- Risulta r = R cos φ
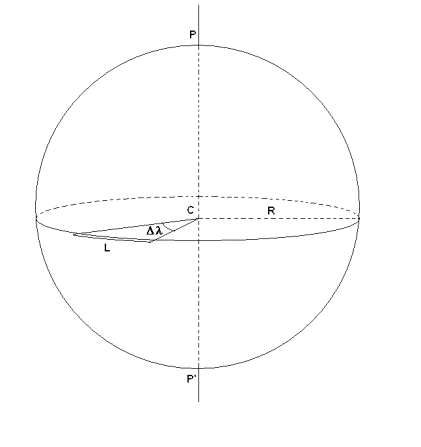
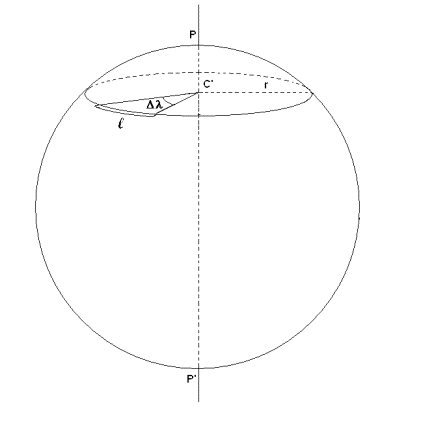
L’EQUATORE
- Un generico arco di equatore è lungo L ed è ampio Δl
- Δλ è l’angolo al centro che insiste sull’arco
L
- R, L, Δ sono tra di loro in relazione :
L = R·Δλrad con R ed L espresse nella
stessa unità di misura
LNM = Δλ’ con L necessariamente espressa
in miglia nautiche
Attenzione: quest’ultima relazione
non vuol dire che miglia e primi sono la stessa cosa, ma semplicemente
che il numero di miglia nautiche è uguale al numero di prim.i
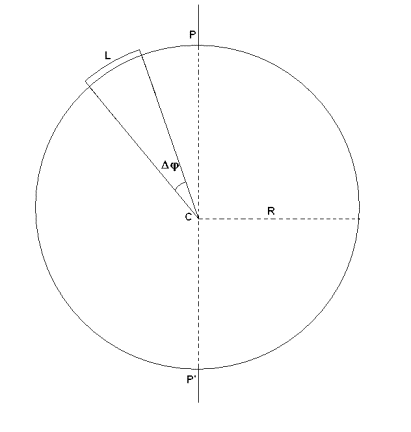
I MERIDIANI
- Un generico arco di meridiano è lungo L ed è ampio Δλ
- Δφ è l’angolo al centro che insiste sull’arco
L
- R, L, Δφ sono tra di loro in relazione :
L = R· Δφrad con R ed L espresse nella
stessa unità di misura
LNM = Δφ’ con L necessariamente espressa
in miglia nautiche
Attenzione: quest’ultima relazione
non vuol dire che miglia e primi sono la stessa cosa, ma semplicemente
che il numero di miglia nautiche è uguale al numero di primi
I PARALLELI
- Un generico arco di parallelo è lungo l ed è ampio
Δλ
- Δλ è l’angolo al centro che insiste sull’arco
l
- r, l, Δλ sono tra di loro in relazione:
l = rΔλrad con r ed l espresse nella
stessa unità di misura
lNM = Δλ’ cosφ
con l espressa in miglia nautiche
Attenzione: quest’ultima relazione
non vuol dire che miglia e primi sono la stessa cosa, ma semplicemente
che il numero di miglia nautiche è uguale al numero di primi
moltiplicato per cosφ
RIEPILOGO FORMULE
- Il raggio della sfera terrestre R si considera pari a 6370
km.
- Il raggio del generico parallelo di latitudine φ r = R
cos φ
- Le relazioni fra lunghezza, ampiezza e raggio degli archi
di circonferenza sulla terra sono:
| Arco di meridiano |
Arco di equatore |
Arco di parallelo |
| L = R Δφrad |
L = R Δλrad |
l = r Δλrad =
R cosφ Δλrad |
| LNM = Δφ’ |
LNM = Δλ’ |
lNM = Δλ’ cos φ |
Tutte le formule possono essere risolte, a seconda dei casi, rispetto
ad uno qualsiasi degli elementi che vi compaiono.
Le formule più usate in navigazione (più “nautiche”) sono quelle
del secondo rigo, che danno le distanze in NM.
ESERCIZI
– 1
Un a/m in volo con TC = 180° alle ore 15:30 sorvola il punto A di
latitudine φ = 18° 30’ N. Calcolare la velocità che dovrà mantenere
per sorvolare l’equatore alle ore 21:00.
Soluzione:
- L’angolo di rotta di 180° fa capire che l’a/m si sposta lungo
un meridiano, verso Sud.
- La distanza che separa l’a/m dall’equatore si calcola con
la formula LNM = Δφ’ .
- Il valore di Δφ ’ si ottiene moltiplicando per 60
il valore di Δφ°.
- In questo caso, l’a/m deve percorrere l’arco di meridiano
compreso fra il punto A e l’equatore, arco che è ampio φA
(vedi definizione di latitudine).
- [Δφ =18° 30’; Δφ’ = 18*60+30 = 1110’ ]
- La distanza che l’a/m deve volare è quindi di 1110 NM.
- Il tempo di volo si calcola per differenza fra gli orari di
sorvolo dell’equatore e di A: 21h 00m
- 15h 30m = 5h 30m
.
- La velocità si calcola come rapporto della distanza sul tempo: GS
= D/FT = 1110 NM/ 5h 30m = 1110 NM/ 5,5h
= 201,8 kts
ESERCIZI – 2
Calcolare le velocità lineare in mph, ed angolare, in gradi
al minuto, che dovrebbe avere un a/m per spostarsi lungo un meridiano,
impiegando da un polo all’altro 36 ore.
Soluzione:
- L’a/m dovrebbe percorrere, da un polo all’altro, una semicirconferenza
massima, ampia 180° e lunga 180*60 NM.
- Si converte questa distanza in miglia statutarie: D = 12428,45
SM
- Si rapporta questa distanza al tempo di volo per trovare GS
= D/FT = 345,23 mph
- Per trovare la velocità angolare si fa il rapporto fra l’ampiezza
dell’arco (180°) e il tempo di volo espresso in minuti. Risulta
ω = Δφ°/min = 0,083°/min.
ESERCIZI – 3
Calcolare le coordinate del punto di arrivo, date quelle del punto
di partenza, l’angolo di rotta, la velocità ed il tempo di volo:
A ( φ = 34° 00’ S, λ = 132° 45’ W ); TC = 360° ; GS =
350 km/h ; FT = 2h 20m .
B (φ = 56° 15’ N, λ = 008° 10’ W ); TC = 90° ; GS = 160
kts ; FT = 3h 05m .
C (φ = 45° 50’ S, λ = 112° 00’ E ); TC = 180° ; GS =
210 mph ; FT = 1h 54m .
D ( φ = 65° 35’ N, λ = 159° 56’ W ); TC = 270° ; GS =
147 m/s ; FT = 5h 42m .
Soluzione
- Si convertono tutte le velocità in kts e si calcolano le distanze
in NM usando la formula D = GS * FT.
- I risultati, arrotondati al miglio intero, sono:
DAA’ = 441 NM ; DBB’ = 493 NM ;
DCC’ = 347 NM ; DDD’ = 1629 NM .
- Lo spostamento AA’ è per meridiano verso Nord, corrisponde
a Δφ = 441’ N ; Δλ è nullo.
- Lo spostamento BB’ è per parallelo verso Est, corrisponde
a Δλ = (493/cosφ)’ E ; Δφ è nullo.
- Lo spostamento CC’ è per meridiano verso Sud, corrisponde
a Δφ = 347’ S ; Δλ è nullo.
- Lo spostamento DD’ è per parallelo verso Ovest, corrisponde
a Δλ = (1629/cosφ)’ W ; Δφ è nullo.
- Le coordinate dei punti di arrivo si calcolano con le formule
φP’ = φPΔφP’P;
λP’ = λP + ΔλP’P
- Risultati approssimati al primo di arco:
A’ ( φ = 26° 39’ S, λ = 132° 45’ W ); B’ ( Φ
= 56° 15’ N, λ = 006° 37’ E ); C’ ( φ = 51° 37’ S,
λ = 112° 00’ E ); D’ ( φ = 65° 35’ N, λ =
134° 23’ E );
ESERCIZI – 4
Calcolare a quali latitudini gli archi di parallelo compreso fra
i meridiani 160° 30’ E e 167° 10’ W sono lunghi:
2500 km ; 695 SM ; 800 km ; 300.000 ft
Soluzione
- Conviene convertire tutte le distanze date in NM. Si ottiene:
D1 = 1349,9 NM ; D2 = 603,9 NM ; D3
= 432 NM ; D4 = 49,4 NM.
- Si calcola il Δλ fra i due meridiani, che risulta
di 32° 20’ .
- Per ciascuna distanza, si applica la formula dell’arco di
parallelo risolvendola rispetto a φ: φ = arccos ( D
/ Δλ)
- Le latitudini richieste sono rispettivamente: φ1
= 45° 54’ 25” ; φ2 = 71° 51’ 47” ; φ3
= 77° 08’ ; φ4 = 88° 32’ 27”
- Nota: i segni delle latitudini sono stati omessi perché le
stesse lunghezze si ritrovano sui paralleli sia Nord che Sud.
ESERCIZI – 5
Un a/m partendo dall’equatore percorre un arco di meridiano, spostandosi
con velocità angolare 0,15 rad/h . Calcolare la sua velocità
lineare in m/s, e dopo quanto tempo sorvolerà il parallelo
di latitudine 22°.
Soluzione:
- Si può calcolare la distanza percorsa dall’a/m in 1 ora direttamente
in km:
L = R Δφrad = 955,5 km
- Per convertire la velocità in m/s bisogna moltiplicare per
1000 e dividere per 3600, ottenendo GS = 265,4 m/s.
- Il parallelo di latitudine 22° dista dall’equatore 22*60
= 1320 NM
- Per calcolare il FT distanza e velocità devono avere unità
di misura coerenti, bisogna allora convertire 1320 NM in km
oppure la velocità in kts
- Il FT si calcola con FT = D/GS = 2h 33m
30s .
ESERCIZI - 6
Un a/m parte alle ore 10:20 dal punto A ( φ = 57° 24’ S , λ
= 169° 50’ W), diretto con rotta costante a B ( φ = 57° 24’
S , λ = 143° 46’ E). è previsto un tempo di volo pari a
4h 10m.
Determinare l’angolo di rotta, la velocità dell’a/m in km/h, e l’ora
di sorvolo dell’antimeridiano di Greenwich.
Soluzione:
- A e B si trovano sullo stesso parallelo, il volo si svolgerà
con rotta 90° oppure 270°.
- Si calcola il ΔλBA = λB
- λA = 46° 24’ W
- Dal segno del ΔλBA si capisce che
l’angolo di rotta sarà TC= 270°
- Si calcola la distanza AB con la formula D = Δλ’
cosφ = ~ 1500 NM
- Si calcola la velocità con la formula GS = D/FT = 360 kts
= 666,7 km/h.
- La lunghezza dell’arco di parallelo compreso fra A e l’antimeridiano
di Greenwich si calcola con la stessa formula vista prima per
la distanza AB: ΔλG’A = 10° 10’ W ,
AG’ = 328,65 NM (nota: G’ è il punto del percorso AB sull’antimeridiano
di Greenwich)
- Il tempo di volo da A a G’ si calcola con FT = D/GS = 0h
54m 47s
- Sommando il FT all’orario di partenza, si trova l’ora di
sorvolo di G’ , 11:14:47
ESERCIZI – 7
Dal punto A di longitudine λ = 34° 45’ E e distante dal polo
Nord 2460 NM, un a/m si sposta con TC = 360°, GS = 296 kts, per
FT = 3h 45m , giungendo a B.
Da B prosegue per parallelo verso W fino al punto C sul meridiano
λ = 15° 38’ E. Calcolare la latitudine di A e di C, la distanza
totale percorsa in km ed il FT complessivo da A a C
Soluzione
- La latitudine di A si calcola considerando che la sua colatitudine
(90° - φ) è pari a 2460’; risulta φA = 49°
00’ N
- Si calcola la distanza AB = GS*FT = 1110 NM; siccome lo spostamento
avviene per meridiano verso Nord, si ha ΔφBA
= 18° 30’ N e quindi φB = φC =
φA + ΔφBA = 67° 30’ N
- Si calcola il ΔλCB, tenendo conto
che A e B si trovano sullo stesso meridiano. ΔλCB
= 19° 07’
- Si calcola la distanza BC con la formula dell’arco di parallelo
ottenendo BC = 438,9 NM.
- Si calcola il FTBC = D/GS = ~ 1h 29m
;
- La distanza totale percorsa risulta 1548,9 NM = 2868,56 km
- Il FT totale risulta di 5h 14m
ESERCIZI – 8
Un a/m sorvola il punto A (φ = 68° 18’ N , λ = 178° 00’
W) e si sposta verso Sud percorrendo in 41 minuti la distanza di
224 km fino al punto B. Quindi assume TC = 270° e con velocità costante
si sposta di Δλ = 12° 37’. Calcolare le coordinate
del punto finale, la velocità espressa in nodi e il FT totale.
Soluzione:
- Si converte la distanza sulla prima tratta in NM: D1
= 120,95 NM
- Si calcola la velocità in nodi rapportando D1 al
FT1 = 41 min. --> GS= 177 kts
- La prima tratta è un arco di meridiano ampio Δφ
= 120.95’ S =~ 121’ S = 2° 01’ S
- Si calcola la latitudine di B φB = φA
+ ΔφBA = 66° 17’ N (B ha la stessa longitudine
di A)
- Si calcola la distanza sulla seconda tratta come arco di parallelo
D2 = Δλ’ cosφ = 304,47 NM attenzione:
la latitudine è quella di B
- Si calcola il FT sulla seconda tratta FT2 = D2/GS
= 1h 43m .
- Si sommano i FT per ottenere il FT totale: --> FTT
= 2h 24m.
- La latitudine del punto finale è la stessa di B, perché la
seconda tratta è per parallelo
- Si calcola la longitudine del punto finale C : λC
= λB + ΔλCB = 169°
23’ E.
ESERCIZI – 9
Due aa/mm si trovano sulla verticale del medesimo punto, sul meridiano
di longitudine 015° 00’ E, alla latitudine φ = 25°00’ N. L’a/m
1 si sposta con TC1 = 90°, GS1 = 400k
; l’a/m 2 si sposta con TC2 = 270°, GS2 =
300k . Determinare su quale meridiano si incroceranno
di nuovo.
Soluzione
- Gli aa/mm percorrono lo stesso parallelo, in direzioni opposte
- Il FT può essere calcolato rapportando la lunghezza del parallelo
alla velocità relativa dei due aa/mm: FT = (360*60*cosφ/(GS1
+ GS2) = (360*60*cos25)/700
- In alternativa, l’esercizio si può risolvere considerando
le velocità angolari degli aa/mm
- In 1 ora l’a/m 1 percorre un arco lungo 400 NM e ampio Δλ1’
= D1/cosφ = 441,3’ E
- In 1 ora l’a/m 2 percorre un arco lungo 300 NM e ampio Δλ2’
= D2/cosφ = 331’ W
- Gli aa/mm hanno inizialmente un Δλ di 0° che
aumenta ogni ora di |Δλ1| + |Δλ2|
= 12° 52’ 22”
- Si incroceranno di nuovo quando il Δλ fra di
loro sarà diventato di 360°, e cioè dopo FT = 360°/( |Δλ1|
+ |Δλ2|) = 27h 57m
58s
- In questo FT l’a/m 1 si sposta di D = GS*FT= 11186,4 NM che
corrispondono a Δλ’ = D/cosφ = 205° 42’ 50”
E.
- Sommando questo Δλ alla longitudine iniziale
si trova la long. del meridiano dove i due aa/mm si reincroceranno:
λ = 139° 17’ 10” W.
ESERCIZI - 10
Un a/m deve volare dal punto A(φ = 39° 43’ N , λ = 104°
26’ E) al punto B(φ = 23° 23’ N , λ = 126° 32’ E ),
spostandosi prima per meridiano e poi per parallelo. Il volo si
svolgerà a velocità costante 347 kts. Calcolare la distanza totale
percorsa ed il tempo di volo.
Soluzione
- Si calcolano le coordinate relative di B rispetto ad A :
ΔφBA = 16° 20’ S ; ΔλlBA
= 22° 06’ E
- La prima tratta, per meridiano verso S avrà TC = 180°, DNM
= Δφ‘ = 980 NM
- La seconda tratta, per parallelo verso Est, avrà TC = 90°;
la latitudine sarà quella di B, e la lunghezza DNM =
Δλ’ cos φ = 1217 NM
- La distanza totale percorsa è la somma delle distanze parziali,
2197 NM
- Il tempo di volo calcolato con la formula FT = D/GS = 6h
19m 53s.
|