Itaer De Pinedo - Lavori e pubblicazioni multimediali

TRASFORMAZIONI DI PRUE E RILEVAMENTI

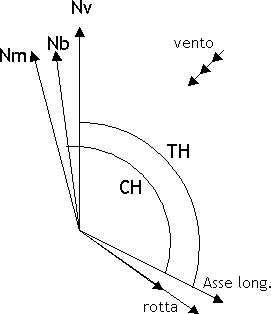
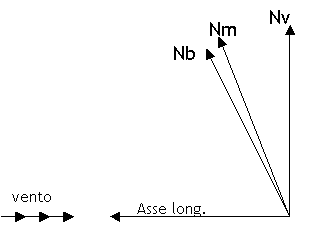
Le direzioni di riferimento che si considerano in navigazione sono:

Nord geografico o vero	N_v
Nord magnetico	N_m
Nord bussola	N_b
asse longitudinale dell'a/m

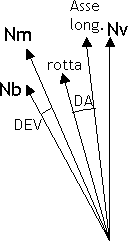
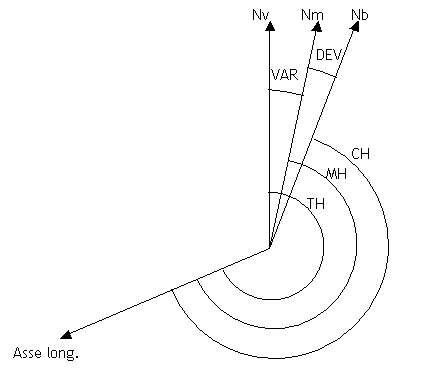
si possono considerare "esatte" le direzioni riferite al Nord vero, e man mano più "erronee" quelle riferite al Nord magnetico e al Nord bussola.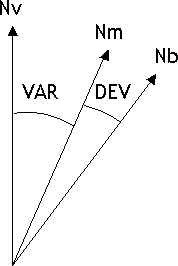

Le direzioni di riferimento formano fra di loro gli angoli:

VAR

DEV

Il segno di questi angoli indica la posizione del Nord più erroneo rispetto a quello più esatto:

VAR

DEV

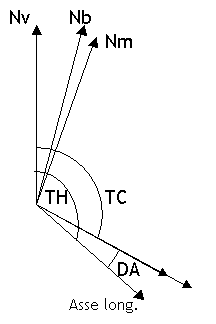
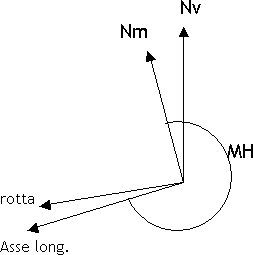
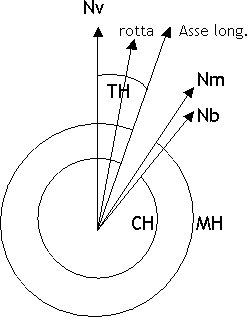
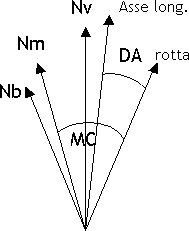
Prue, rotte e rilevamenti si individuano tramite l'angolo corrispondente, misurato sempre in senso orario a partire dalla direzione di riferimento. Le prue, le rotte e i rilevamenti si indicano con sigle di due lettere: la prima indica da dove si inizia a contare l'angolo e può essere:

T =	True che sta per Nord vero
M =	Magnetic che sta per Nord magnetico
C =	Compass che sta per Nord bussola

La seconda lettera può essere:

H =	Heading per indicare la prua, direzione dell'asse longitudinale dell'a/m
C =	Course per indicare la rotta, direzione dello spostamento dell'a/m
B =	Bearing per indicare il rilevamento di un oggetto.

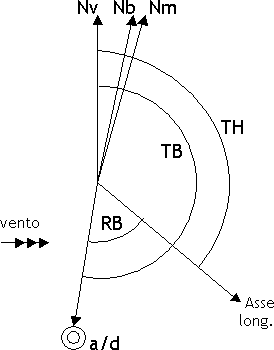
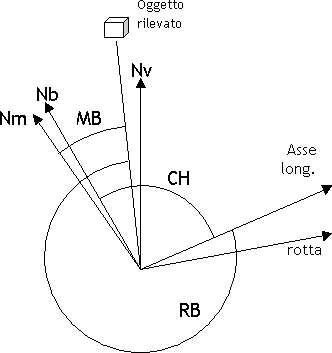
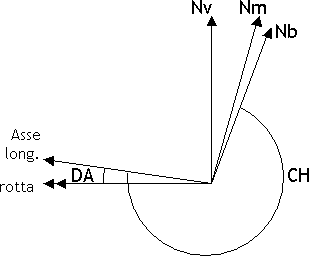
Il rilevamento può essere misurato a partire dell'asse longitudinale dell'a/m; in tal caso prende il nome di rilevamento polare, in sigla RB Relative Bearing oppure Rilpo. Si ha che TB = TH + RB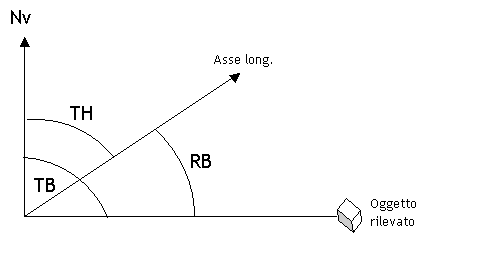

L'asse longitudinale dell'a/m e la direzione della rotta formano un angolo chiamato deriva, in sigla DA = Drift Angle, dovuto all'azione del vento. Alla deriva si attribuisce segno: positivo, e si indica con la lettera R = right, destra, se la rotta è a destra della prua; negativo, e si indica con la lettera L = left, sinistra, se la rotta è a sinistra della prua. Si ha che TC = TH + DA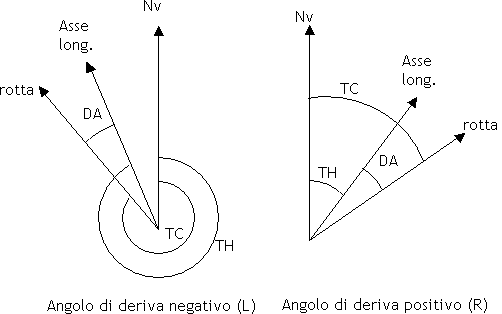

"Trasformare" una prua o un rilevamento vuol dire riferire la prua o il rilevamento ad una direzione di riferimento diversa da quella data; ad esempio passare dalla prua vera a quella bussola, oppure dal rilevamento magnetico a quello vero.

Si chiamano:

conversioni

correzioni

	TH		TC		TB
	MH		MC		MB
	CH				CB
correzioni		conversioni		correzioni		conversioni

Per eseguire le trasformazioni vale la regola:

per correggere = calcolare un valore esatto partendo da uno più erroneo DEV e/o VAR si aggiungono

per convertire = calcolare un valore più erroneo partendo da uno esatto DEV e/o VAR si sottraggono

correzioni

TH = MH + VAR

TH = CH + DEV + VAR

MH = CH + DEV

TC = MC + VAR

TB = MB + VAR

TB = CB + DEV + VAR

MB = CB + DEV

conversioni

MH = TH - VAR

CH = TH - DEV - VAR

CH = MH - DEV

MC = TC - VAR

MB = TB - VAR

CB = TB - DEV - VAR

CB = MB - DEV

Tutte le formule fin qui viste vanno considerate algebriche: VAR, DEV e DA devono essere inserite nel calcolo con il loro segno; l'angolo di DEV è generalmente piccolo; l'angolo di VAR non può superare 180°; tutti gli angoli di prue, rotte e rilevamenti si contano in senso orario da 0° a 360°, e quindi:

se il risultato è negativo, bisogna aggiungere 360° es. TC = - 23° = -23°+360° = 337°
se il risultato è >360°, bisogna sottrarre questo valore, es. MH = 368° = 368°-360°= 8°

ESEMPI ED ESERCIZI

Nota: le direzioni riportate nei grafici sono solo indicative

Esercizio 1

Dati: CH = 130°, DEV = -3°, VAR = 18° E, DA = 9°L, calcolare la TC dell'a/m e rappresentare in un grafico tutte le direzioni.

Soluzione:

TC	= TH + DA
	= CH + DEV +VAR + DA
	= 130°+(-3°)+(+18°)+(-9°) = 136°

Risultano inoltre:

MH = 127°, TH = 145°

Esercizio 2

Un a/m deve volare da A a B con TC = 260°, in presenza di vento che causa un angolo di deriva pari a 8°R, in una zona dove VAR = 13°W. La bussola si suppone perfettamente compensata. Calcolare il valore da leggere ala bussola.

Soluzione:

alla bussola normalmente si legge il valore CH, ma se la compensazione è perfetta, si può considerare DEV = 0°; in tal caso, CH = MH.

Si calcola:

TH = TC - DA = 260°- (+8°) = 252°

MH = TH - VAR = 252°- (-13°) = 265°

Esercizio 3

Un pilota vola mantenendo costante l'indicazione della bussola su 350°; sapendo che la sua TC = 010°, che DEV = +3° e DA = 12°L, determinare l'angolo di VAR.

Soluzione:

la lettura della bussola fornisce l'angolo CH. Si calcola:

TH = TC - DA = 10° - (-12°) = 22°

MH = CH + DEV = 350°+ (+3°) = 353°

VAR = TH - MH = 22° - 353° =
= - 331° = 360° - 331° = +29° = 29°E

Esercizio 4

Sapendo che DEV = -4°, MC = 040°, TH = 005°, CH = 025°, calcolare l'angolo di deriva.

Soluzione:

MH = CH + DEV = 25° + (-4°) = 21°

VAR = TH - MH = 5° - 21° = -16° = 16°W

TC = MC + VAR = 40° + (-16°) = 24°

DA = TC - TH = 24° - 5° = +19° = 19°R

Esercizio 5

Sapendo che TC = 345°, MC = 003°, MH = 015°, CH = 020°, calcolare l'angolo di deriva e l'angolo di DEV.

Soluzione:

VAR = TC - MC = 345° - 003° = +342° = 342° - 360° = -18° = 18°W

TH = MH + VAR = 015°+(-18°) = - 3° = 357°

DA = TC - TH = 345° - 357° = -12° = 12°L

DEV = MH - CH = 15° - 20° = -5°

Esercizio 6

In assenza di vento un a/m è in volo in una zona dove la VAR = 23°E, con CH = 120°, DEV = -4°. Il pilota rileva un aerodromo per RB = 45°; calcolare la rotta vera di avvicinamento all'a/d. Stabilire inoltre, nel caso in cui in zona soffi un vento da ovest, se la prua di avvicinamento dovrà essere minore o maggiore della rotta.

Soluzione:

TH = CH + DEV + VAR = = 120° +(-4°) +(+23°) = 139°
TB = TH + RB = 139° + 45° = 184°

La rotta di avvicinamento (TC) è uguale al rilevamento vero. Per percorrerla, in assenza di vento l'a/m dovrà assumere TH = TB.

In presenza di vento da ovest, bisognerà assumere TH > TC, per contrastare il vento che proviene da destra.

Esercizio 7

In volo con TC = 74°, DA = 18°R, VAR = 36°W, DEV = +3°, si osserva un oggetto per RB = 300°. Calcolare i corrispondenti TB, MB e il valore letto alla bussola.

Soluzione:

TH = TC - DA = 74°- (+18°) = 56°

TB = TH + RB = 56° + 300° = 356°

MB = TB - VAR = 356°- ( -36) = 392°= 32°

CH = TH - DEV - VAR = 56°- ( +3°) - (-36°) = 89°

Esercizio 8

In volo con TC = 270°, GS = 240^k, CH = 255°, DEV = +2°, VAR = 27°E, si sorvola il punto di coordinate φ = 48°00' N, λ = 167° 45'W. Calcolare l'angolo di deriva, ed il FT per sorvolare il meridiano di longitudine 157° 52'E. Stabilire se il vento proviene da N o S.

Soluzione:

TH = CH + DEV + VAR = = 255° +(+2°) +(+27°) = 284°

DA = TC - TH = 270°- 284° = = -14°= 14°L

Il vento proviene da destra, quindi da N

Δλ = λ_B - λ_A = 34° 23' W = 2063'

D = Δλ' cosφ = 1380,4 NM
FT = D/GS = 5^h 45^m 06^s

Esercizio 9

Calcolare i valori di DEV e VAR sapendo che CH = 145°, TH = 137°, e che i coefficienti del c.m.b. sono A = 0°, B = +5°, C = -2°, D = 0°, E = +1°. L'a/m vola in presenza di vento da NE che causa una deriva di 10°. Stabilire il segno dell'angolo di deriva e la TC.

Soluzione:

DEV = A + B senCH + C cosCH + D sen2CH + E cos2CH = +4,8° = ~ +5°

MH = CH + DEV = 150°

VAR = TH - MH = - 13° = 13°W Il vento proviene da sinistra ->

l'angolo DA è positivo

DA = 10°R

TC = TH + DA = 147°

Esercizio 10

Si vuole volare dal punto A (φ = 54° 11' N, λ = 127° 48' E ) al punto B (φ = 54° 11' N, λ = 121° 32' E ) con rotta costante, impiegando FT = 1^h 45^m. Il campo magnetico di bordo provoca un deviazione di 3° a sinistra, e la declinazione magnetica nella zona di volo è 27°W ; il vento è frontale, di intensità 15^k. Calcolare l'indicazione della bussola e la velocità che dovrà avere l'a/m.

Soluzione: il vento frontale non provoca deriva, ma "rallenta" l'a/m rispetto al suolo. Dalla traccia si evince che DEV = -3°, VAR = -27° e DA = 0°. La TC si ricava dal confronto delle coordinate di A e B: TC = TH = 270°. La distanza AB si calcola con la formula dell'arco di parallelo: D = 220 NM.
La velocità al suolo dovrà essere GS = D/FT = 126^k. La velocità dell'a/m dovrà essere di 126 + 15 = 141^k per contrastare il vento frontale. Per la CH: CH = TH - DEV - VAR = 270° + 3° + 27° = 300°

-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-