Analizziamo per prime le disposizioni
D _{( n, k )}
Le disposizioni sono il numero
dei possibili gruppi  che si possono
formare con n elementi presi k alla volta,
in modo che ogni gruppo sia
distinto da un altro per :
a) la presenza di almeno un elemento diverso
b)  l'ordine degli elementi nel gruppo
 Esempio
Un segnalatore
che abbia a disposizione sei bandierine diverse
deve comporre messaggi in codice
ma ogni singolo messaggio
può essere composto solo da  tre bandierine.
le D _{( 6, 3 )}
rappresenta il numero massimo, di messaggi
tra loro diversi, che si possono comporre.
I messaggi si distinguono sia
per differenza di bandierine
che per l'ordine in cui sono esposte,
(ordine diverso messaggio diverso).
.
PER DIMOSTRARE CHE
.
D_{( n, k )}= n·(n-1)·(n-2)·...(n-k+1)
Inizieremo il  percorso proponendo
come modello: un urnacontenente
quattro palline (n = 4) ognuna delle quali contrassegnata
da un numero intero. Per comodità diremo:
dal numero 1 al numero 4.
Ci porremo alcune domande via, via più
complesse utilizzando le risposte dei casi
elementari per poter definire le risposte alle
domande successive.
.
1° domanda:
Se si estrae una sola  pallina (k=1)
quante possono essere le estrazioni diverse?
D_{( 4, 1 )}=    ?
.
Risposta
ogni pallina può venire estratta e quindi
il numero delle estrazioni sarà,
ovviamente, 4 quante sonole le  palline
tra loro diverse.
.
2° domanda:
Se si estraggono due  palline
quante possono essere le estrazioni diverse?
D_{( 4, 2 )}=    ?
.
Risposta
Utilizzando in maniera costruttiva
la risposta  del primo caso.
Se rappresentiamo con la nascita di
quattroalberi  dal seme delle
quattro estrazioni precedenti ed interpretiamo
la nuova estrazione come una nuova
stagione vegetativa delle nostre quattro piante
che  consentirà ad ogni albero
di generare tanti rami quanti
sono i numeri che non sono gia
stati utilizzati.

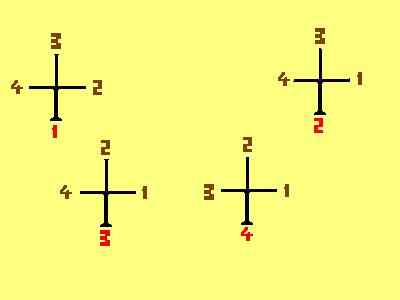
il numero in rosso è il numero che
distingue ogni albero
(numero corrispondente)
(alla prima pallina estratta)
i numeri in marrone quelli di tutti i rami possibili
nella vegetazione succesiva.
(numeri corrispondenti )
(alla pallina estratta come seconda)
La risposta è il numero
degli alberi moltiplicato per
il numero dei rami dell'ultima vegetazione
In generale la risposta è
D_{( 4, 2 )}= 4  · 3=  12
nel caso di   n  palline
D_{( n , 2 )}= n·(n-1)
.
3° domanda:
Se si estraggono tre  palline
quante possono essere le estrazioni diverse?
D_{( 4, 3 )}=   ?
.
Risposta
nel nostro modello con quattro alberi
con la terza vegetazione (estrazione)
ogni ramo produrrà tanti nuovi  rametti quanti
sono i numeri che non sono gia
stati utilizzati, nel nostro caso 2 .

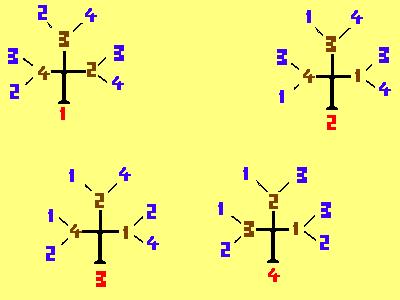
i quattro alberi
hanno tre grandi rami
ognuno dei quali ha due rametti
i rametti sono in totale
D_{( 4, 3 )}=  n·(n-1)·(n-2)·...(n-k+1)=
=n·(n-1)·(n-3+1)= 4·(4-1)·(4-2)=
4 · 3 · 2 = 24
In generale il numero totale delle palline ( 4)
per il numero delle rimanenti  (4-1= 3)
per il numero delle restanti  (3-1= 2)
.
 4° domanda:
Se si estraggono quattro  palline
quante possono essere le estrazioni diverse?
D_{( 4, 4 )}= P_{(4 )} =
nel nostro modello
con quattro alberi

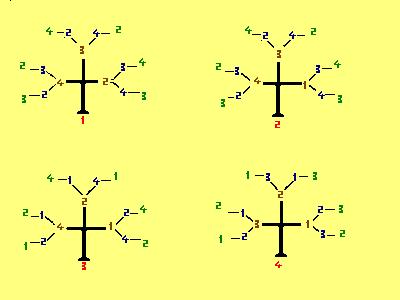
generalizzando
D_{( 4, 4 )}= P_{(4 )} =  n·(n-1)·(n-2)·...·2·1=
= n! = 4·3·2·1 =24
Abbiamo così scoperto anche che
D_{( 4, 3 )}= D_{( 4, 4 )}= P_{(4 )} =
e che in generale
D_{( n,n-1 )}= D_{( n, n )}= P_{(n )}