S
O R T
Algoritmi di ordinamento
(di Maurizio Mauri)
Algoritmi di ordinamento
(di Maurizio Mauri)
| Bubble Sort |
| Bidirectional Bubble Sort |
| Selection Sort |
| Insertion Sort |
| Shell Sort |
| Quick Sort |
| Quick Sort 2 |
| Merge Sort |
| Bucket Sort |
| Heap Sort |
Per ordinare un vettore
si possono usare i metodi più disparati. Alcuni semplici
e intuitivi; direi che ognuno di noi forse potrebbe inventare
un nuovo metodo. Però difficilmente questi metodi
avranno l'efficienza di altri metodi più complessi.
Ci potremo sorprendere dell'estrema velocità dello
Shell Sort o del Quick Sort, anche centinaia o migliaia
di volte maggiore di quella del Bubble sort.
Bubble Sort
Iniziamo con l'algoritmo più semplice, il Bubble Sort, ordinamento a bolle: come le bollicine d'aria nell'acqua che risalgono lentamente alla supeficie, gli elementi più grandi di un vettore vengono pian piano spostati verso l'alto fino a raggiungere la loro posizione ordinata.
L'algoritmo consiste in pratica in questi passi:
Bidirectional Bubble Sort
Un piccolo miglioramento del Bubble Sort si ha con il Bidirectional Bubble Sort. Con questo algoritmo si fanno una doppia serie di confronti per ogni ciclo: prima si fa "risalire" il più grande dei numeri, poi si fa "scendere" il più piccolo dei numeri.
Facciamo un esempio con lo stesso vettore usato in precedenza:
Insertion Sort
L'Insertion Sort è un metodo con cui, a partire dal secondo elemento di un array, viene effettuato il confronto con tutti gli elementi precedenti. Nel caso che venga trovato un valore più grande, tutti gli elementi a partire da quello trovato, vengono fatti slittare di un posto, per far spazio all'elemento che deve essere inserito.
Viene effettuato lo stesso numero di confronti del Bubble Sort o del Selection Sort, per cui c'è da aspettarsi più o meno la stessa efficienza.
Questo è il programma che effettua un Insertion Sort:
Si faccia attenzione che non è lecito generalizzare troppo questi risultati per concludere che un metodo è sempre, ad esempio, il doppio più veloce di un altro e che sia sempre preferibile. Questi tempi dipendono da troppe variabili: il tipo di computer, il linguaggio usato, il numero di elementi e il tipo di array che si sta ordinando e, in qualche caso, potrebbero dare anche indicazioni diverse.
Per un utile confronto riportiamo, nella tabella che segue, i risultati ottenuti sulla stessa macchina e con le stesse funzioni, ma con un numero di elementi di 5.000.000 (100 volte superiore):
Non sono stati provati gli algoritmi più lenti che avrebbero richiesto parecchie ore di elaborazione.
MergeSort
Il principio ispiratore del MergeSort è lo stesso del Quick Sort e dello ShellSort, cioè quello di dividere in due parti l'array ed effettuare l'ordinare l'ordinamento su due array più piccoli. Però questo algoritmo non si cura che di spezzare preventivamente il vettore in modo che tutti gli elementi più grandi siano da una parte e quelli più piccoli da un'altra; alla fine del sort i due sottoarray dovranno essere rimessi assieme (merged) con un lavoro non indifferente, che farà aumentare notevolmente il tempo.
Descriviamo l'algortmo con il solito esempio di vettore:
Bucket Sort
Il Bucket Sort è un algoritmo che si presta ad ordinare stringhe di lunghezza fissa ed è particolarmente veloce nel caso nel caso che il numero degli elementi sia molto elevato.
Consiste praticamente nel creare tanti gruppi, quanti sono i caratteri ammessi, in modo che in ciascun gruppo vi siano solo gli elementi che hanno lo stesso carattere nell'ultima posizione. Poi si ripete lo stesso procedimento per il penultimo carattere, il terzultimo, e così via. Al termine avremo l'array ordinato.
Ad esempio, supponiamo di dover ordinare le seguenti stringhe numeriche di 3 cifre:
Bubble Sort
Iniziamo con l'algoritmo più semplice, il Bubble Sort, ordinamento a bolle: come le bollicine d'aria nell'acqua che risalgono lentamente alla supeficie, gli elementi più grandi di un vettore vengono pian piano spostati verso l'alto fino a raggiungere la loro posizione ordinata.
L'algoritmo consiste in pratica in questi passi:
- si inizia dal primo elemento di un array e lo si confronta
con quello immediatamente superiore;
- se il primo è più grande del secondo
i due elementi vengono scambiati;
- poi si passa al secondo elemento e lo si confronta
con quello superiore ed eventualmente si scambiano fra
di loro;
- dopo aver confrontato tutti gli elementi si ricomincia
da capo e si effettua un nuovo ciclo di confronti e
di eventuali scambi;
- l'ordinamento termina quando tutti gli elementi sono
ordinati, e cioè quando in un ciclo non viene
scambiato alcun elemento.
| 4 | 3 | 2 | 1 |
Il primo elemento (4) viene prima confrontato
con il secondo (3) e scambiato:
| 3 | 4 | 2 | 1 |
Ora il secondo elemento (sempre il 4)
viene confrontato con il successivo (2) e scambiato:
| 3 | 2 | 4 | 1 |
Infine il 4 viene confrontato con l'ultimo
elemento (1) e scambiato con esso. Il 4, quindi, con una
serie di 3 confronti e 3 scambi viene fatto risalire fino
all'ultima posizione:
| 3 | 2 | 1 | 4 |
Ora si ricomincia il ciclo dei confronti
dal primo elemento (3) che verrà fatto risalire
fino alla penultima posizione:
| 2 | 1 | 3 | 4 |
Infine con un terzo ciclo di confronti
e di scambi (il 2 con l'1) si raggiunge l'ordinamento:
| 1 | 2 | 3 | 4 |
In totale sono stati fatti 3 cicli con
3 confronti nel primo, 2 nel secondo, 1 nel terzo (6 in
totale). Sono stati fatti 3 scambi nel primo ciclo, 2
nel secondo e solo 1 nel terzo; in totale 6 scambi.
Questo è, in realtà, il caso peggiore per il Bubble Sort, quello che richiede il maggior numero di confronti e di scambi. Se il vettore fosse stato trovato già ordinato, sarebbe stato necessario un solo ciclo, in cui saranno effetuati solo confronti (l'assenza di scambi starà ad indicare che il vettore è già ordinato).
Se vogliamo generalizzare, per un vettore di n elementi richiederanno (n - 1) + (n - 2) + ... + 1 confronti, per un totale di n*(n-1) / 2, uguale al numero di scambi massimo.
In pratica il numero di confronti e di scambi cresce con il quadrato del numero degli elementi. Il che vuol dire che, supponendo che sia necessario 1 secondo di tempo per ordinare 1000 elementi, verranno richiesti 100 secondi per ordinarne 10.000 e 10.000 secondi (circa 3 ore) per ordinarne 100.000. Questo fa sì che questo semplice algoritmo non si presti molto ad ordinare un numero elevato di elementi (a meno che questi elementi non si trovino già quasi in ordine).
Ora vediamo un'animazione per visualizzare le operazioni di sort. Per far partire l'animazione clicca sull'immagine:
Questo è, in realtà, il caso peggiore per il Bubble Sort, quello che richiede il maggior numero di confronti e di scambi. Se il vettore fosse stato trovato già ordinato, sarebbe stato necessario un solo ciclo, in cui saranno effetuati solo confronti (l'assenza di scambi starà ad indicare che il vettore è già ordinato).
Se vogliamo generalizzare, per un vettore di n elementi richiederanno (n - 1) + (n - 2) + ... + 1 confronti, per un totale di n*(n-1) / 2, uguale al numero di scambi massimo.
In pratica il numero di confronti e di scambi cresce con il quadrato del numero degli elementi. Il che vuol dire che, supponendo che sia necessario 1 secondo di tempo per ordinare 1000 elementi, verranno richiesti 100 secondi per ordinarne 10.000 e 10.000 secondi (circa 3 ore) per ordinarne 100.000. Questo fa sì che questo semplice algoritmo non si presti molto ad ordinare un numero elevato di elementi (a meno che questi elementi non si trovino già quasi in ordine).
Ora vediamo un'animazione per visualizzare le operazioni di sort. Per far partire l'animazione clicca sull'immagine:
| Bubble Sort |
Facciamo un semplice programmino in
C per implementare questo algoritmo:
void bubblesort(int *a, int n) {
int i, j, temp;}
int swapped = 0;
// effettua (al massimo) n cicli
for (i = n; --i > 0; ) {
swapped = 0;}
for (j = 0; j < i; j++) {
if (a[j] > a[j+1]) {}
// scambia gli elementi}
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
swapped = 1;
if (!swapped)
break;
Bidirectional Bubble Sort
Un piccolo miglioramento del Bubble Sort si ha con il Bidirectional Bubble Sort. Con questo algoritmo si fanno una doppia serie di confronti per ogni ciclo: prima si fa "risalire" il più grande dei numeri, poi si fa "scendere" il più piccolo dei numeri.
Facciamo un esempio con lo stesso vettore usato in precedenza:
| 4 | 3 | 2 | 1 |
Prima si fa risalire il "4"
fino alla sua posizione finale:
| 3 | 2 | 1 | 4 |
Poi si prende il penultimo elemento
(1) e lo si fa ridescendere alla prima posizione:
| 1 | 3 | 2 | 4 |
Poi, si prende il 3 e lo si porta in
penultima posizione. E a questo punto il vettore è
ordinato.
In totale sono stati fatti 3 + 2 + 1 = 6 confronti e lo stesso numero di scambi. In questo caso, il più sfavorevole, non si vedono miglioramenti, ma all'atto pratico, considerando un vettore casuale, si nota un miglioramento attorno al 20%.
Per capire la ragione del miglioramento di prestazioni, rispetto al semplice Bubble Sort, pensiamo ad un vettore del genere:
In totale sono stati fatti 3 + 2 + 1 = 6 confronti e lo stesso numero di scambi. In questo caso, il più sfavorevole, non si vedono miglioramenti, ma all'atto pratico, considerando un vettore casuale, si nota un miglioramento attorno al 20%.
Per capire la ragione del miglioramento di prestazioni, rispetto al semplice Bubble Sort, pensiamo ad un vettore del genere:
| 2 | 3 | 4 | 1 |
È più semplice, in questo
caso, far ridiscendere l'1 in prima posizione (con un
solo cliclo di confronti) piuttosto che far salire gli
altri tre numeri (con tre cicli).
Questa è l'animazione che mostra le operazioni effettuate nel sort:
Questa è l'animazione che mostra le operazioni effettuate nel sort:
| Bidirectional Bubble Sort |
Questo, per concludere, il programmino
in C che implementa l'algoritmo:
void bidir_bubblesort(int *a, int n) {
int i, j, temp;}
int limit = n; int st = -1;
int swapped = 0;
while (st < limit) {
st++;}
limit--;
swapped = 0;
for (j = st; j < limit; j++) {
if (a[j] > a[j+1]) {}
// scambia gli elementi}
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
swapped = 1;
if (!swapped)
break;else
swapped = 0;for (j = limit; --j >= st;) {
if (a[j] > a[j+1]) {}
// scambia gli elementi}
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
swapped = 1;
if (!swapped)
break;
La maggiore complicazione dell'algoritmo
non lo fa preferire ad altri.
Miglioramenti del Bubble Sort
Ulteriori miglioramenti del Bubble Sort si possono ottenere riducendo al minimo gli scambi, quando non sono necessari. Infatti pensiamo al vettore:
Miglioramenti del Bubble Sort
Ulteriori miglioramenti del Bubble Sort si possono ottenere riducendo al minimo gli scambi, quando non sono necessari. Infatti pensiamo al vettore:
| 4 | 1 | 2 | 3 |
Il 4 viene prima scambiato con l'1,
poi col 2 e infine col 3. Sarebbe più far slittare
i 3 elementi più piccoli e inserire il 4 direttamente
in ultima posizione. Questo può essere fatto con
un programma del genere:
void bubblesort1(int *a, int n) {
int i, j, temp;}
int swapped = 0;
// effettua (al massimo) n cicli
for (i = n; --i > 0; ) {
swapped = 0;}
for (j = 0; j < i; j++) {
temp = a[j];}
while (temp > a[j+1] && j < i) {
a[j] = a[j+1];}
j++;
swapped = 1;
a[j] = temp;
if (!swapped)
break;
Questo porta mediamente ad un ulteriore
miglioramento del 10% circa.
Selection Sort
Un difetto del Bubble sort è quello di effettuare scambi inutili. Che utilità ha far risalire un elemento per posizionarlo poi in ultima posizione? Con il Selection Sort si cerca di superare questo difetto, ricercando prima l'elemento più grande (o il più piccolo) e poi scambiarlo.
L'algoritmo, in pratica si articola nei seguenti passi:
Selection Sort
Un difetto del Bubble sort è quello di effettuare scambi inutili. Che utilità ha far risalire un elemento per posizionarlo poi in ultima posizione? Con il Selection Sort si cerca di superare questo difetto, ricercando prima l'elemento più grande (o il più piccolo) e poi scambiarlo.
L'algoritmo, in pratica si articola nei seguenti passi:
- si prende il primo elemento e lo si confronta con
tutti quelli successivi per determinare quale di questi
è il più piccolo;
- si scambia, quindi il primo elemento con quello
più piccolo trovato;
- si continua con gli elementi successivi.
| 4 | 3 | 2 | 1 |
Si trova prima il minimo dei 4 elementi
(facendo 3 confronti). Alla fine, trovato che l'1 è
l'elemento più piccolo, si scambia con il 4, ed
avremo:
| 1 | 3 | 2 | 4 |
In questo caso, rispetto al Bubble Sort
si sono risparmiati 2 scambi.
Poi si continua determinando il minimo degli elementi a partire dal secondo. Questo minimo, il 2, si scambia con il 3, ed avremo:
Poi si continua determinando il minimo degli elementi a partire dal secondo. Questo minimo, il 2, si scambia con il 3, ed avremo:
| 1 | 2 | 3 | 4 |
Cioè il vettore è già
ordinato, ma non abbiamo modo di verificarlo e dovremo
continuare il confronto del terzo elemento con il successivo.
In totale abbiamo avuto 3 + 2 + 1 = 6 confronti e soltanto 2 scambi con notevole vantaggio rispetto al Bubble Sort.
Però in realtà la situazione non è sempre così favorevole. La situazione peggiore si ha quando quasi tutti gli elementi sono ordinati, escluso il primo, ad esempio:
In totale abbiamo avuto 3 + 2 + 1 = 6 confronti e soltanto 2 scambi con notevole vantaggio rispetto al Bubble Sort.
Però in realtà la situazione non è sempre così favorevole. La situazione peggiore si ha quando quasi tutti gli elementi sono ordinati, escluso il primo, ad esempio:
| 4 | 1 | 2 | 3 |
In questo caso, il Selection Sort richiederà
esattamente lo stesso numero di scambi del Bubble Sort.
Un altro difetto si ha nel fatto che non esiste alcun modo per verificare che il vettore sia già ordinato se non effettuando tutti i controlli previsti.
Mediamente, con un vettore casuale, il Selection Sort risulta un po' più veloce del Bubble Sort, impiegando anche meno della metà del tempo.
Questo è il programma che implementa l'algoritmo:
Un altro difetto si ha nel fatto che non esiste alcun modo per verificare che il vettore sia già ordinato se non effettuando tutti i controlli previsti.
Mediamente, con un vettore casuale, il Selection Sort risulta un po' più veloce del Bubble Sort, impiegando anche meno della metà del tempo.
Questo è il programma che implementa l'algoritmo:
| Selection Sort |
void selectionsort(int *a, int n) {
int i, j, ix, mx;}
for (i = 0; i < n - 1; i++) {
mx = a[i];}
ix = i;
for (j = i + 1; j < n; j++)
if (a[j] > mx) {if (i != ix) {
mx = a[j];}
ix = j;
a[ix] = a[i];}
a[i] = mx;
Insertion Sort
L'Insertion Sort è un metodo con cui, a partire dal secondo elemento di un array, viene effettuato il confronto con tutti gli elementi precedenti. Nel caso che venga trovato un valore più grande, tutti gli elementi a partire da quello trovato, vengono fatti slittare di un posto, per far spazio all'elemento che deve essere inserito.
Viene effettuato lo stesso numero di confronti del Bubble Sort o del Selection Sort, per cui c'è da aspettarsi più o meno la stessa efficienza.
Questo è il programma che effettua un Insertion Sort:
| Insertion Sort |
void insertsort(int *a, int n) {
int i, j, k, temp;}
for (i = 1; i < n; i++) {
j = i;}
temp = a[i];
while (j > 0 && temp <= a[j - 1]) {
a[j] = a[j - 1];}
j--;
a[j] = temp;
L'algoritmo è estremamente semplice,
ma ha il suo punto debole sull'enorme numero di spostamenti
che deve fare per far posto ad un nuovo elemento.
Ad esempio, se prendiamo il vettore:
Ad esempio, se prendiamo il vettore:
| 6 | 5 | 4 | 3 | 2 | 1 |
Prima si confronta il 5 con il 6 e vengono
scambiati. Poi il 4, in terza posizione, viene confrontato
prima con il 6, in seconda posizione, e con il 5, in prima
posizione; il 5 e il 6 vengono fatti slittare di un posto
e il 4 viene messo in prima posizione. E così via.
Vediamo che vengono effettuati 1 + 2 + 3 + 4 + 5 = 15 confronti: n * (n - 1) / 2 confronti; dopo ogni ciclo di confronti viene effettuato uno scambio e diversi slittamenti di numero pari a quello dei confronti (5 scambi e lo slittamento di 10 numeri).
Questo metodo si presta particolarmente nel caso di vettori che risultano già ordinati, anche parzialmente, quando si renda necessario aggiungere un nuovo elemento al vettore.
Shell Sort
Lo Shell Sort costituisce praticamente un miglioramento dell'Insertion Sort, su cui si basa. Il miglioramento consiste nel cercare di effettuare il minor numero di slittamenti possibili effettuando preventivamente degli ordinamenti parziali.
Facciamo un esempio per spiegare l'algoritmo, considerando questo vettore:
Vediamo che vengono effettuati 1 + 2 + 3 + 4 + 5 = 15 confronti: n * (n - 1) / 2 confronti; dopo ogni ciclo di confronti viene effettuato uno scambio e diversi slittamenti di numero pari a quello dei confronti (5 scambi e lo slittamento di 10 numeri).
Questo metodo si presta particolarmente nel caso di vettori che risultano già ordinati, anche parzialmente, quando si renda necessario aggiungere un nuovo elemento al vettore.
Shell Sort
Lo Shell Sort costituisce praticamente un miglioramento dell'Insertion Sort, su cui si basa. Il miglioramento consiste nel cercare di effettuare il minor numero di slittamenti possibili effettuando preventivamente degli ordinamenti parziali.
Facciamo un esempio per spiegare l'algoritmo, considerando questo vettore:
| 6 | 5 | 4 | 3 | 2 | 1 |
Dividiamo il vettore in due parti uguali.
In tal modo, in realtà, abbiamo creato tre sottovettori,
di due elementi ognuno. Il primo sottovettore è
composto da 6 e 3 (il primo elemento di ognuna delle due
parti); il secondo sottovettore è formato da 5
e 2; il terzo da 4 e 1.
Ordiniamo ora questi 3 sottovettori, con il metodo di Insertion Sort, e otteniamo:
Ordiniamo ora questi 3 sottovettori, con il metodo di Insertion Sort, e otteniamo:
| 3 | 2 | 1 | 6 | 5 | 4 |
Per arrivare a questo risultato sono
stati necessari 3 confronti e 3 scambi.
Terminato questo primo ciclo di confronti e di scambi si suddivide il vettore in ulteriori 2 parti. Nel nostro esempio ogni parte era di 3 elementi; dividendo per 2 si deve prendere la parte intera del risultato (1); per cui avremo ogni parte composta da 1 solo elemento.
Ora il metodo diventa identico all'Insertion Sort: il 2 verrà confrontato e scambiato con il 3; l'1 verrà confrontato prima col 3 e poi col 2; questi due verranno fatti slittare e l'1 verrà messo al primo posto. I primi 3 elementi sono stati ordinati con 2 confronti, 2 scambi e 2 slittamenti.
Per gli ulteriori 3 elementi saranno necessari 3 confronti, 2 scambi e 2 slittamenti. In totale: 3 + 2 + 3 = 8 confronti, 3 + 2 + 2 = 7 scambi, 2 + 2 = 4 slittamenti. Un discreto miglioramento rispetto al metodo precedente.
In realtà questo algoritmo si dimostra enormemente superiore ai precedenti con un numero elevato di elementi da ordinare.
Questo è il programma che implementa l'algoritmo:
Terminato questo primo ciclo di confronti e di scambi si suddivide il vettore in ulteriori 2 parti. Nel nostro esempio ogni parte era di 3 elementi; dividendo per 2 si deve prendere la parte intera del risultato (1); per cui avremo ogni parte composta da 1 solo elemento.
Ora il metodo diventa identico all'Insertion Sort: il 2 verrà confrontato e scambiato con il 3; l'1 verrà confrontato prima col 3 e poi col 2; questi due verranno fatti slittare e l'1 verrà messo al primo posto. I primi 3 elementi sono stati ordinati con 2 confronti, 2 scambi e 2 slittamenti.
Per gli ulteriori 3 elementi saranno necessari 3 confronti, 2 scambi e 2 slittamenti. In totale: 3 + 2 + 3 = 8 confronti, 3 + 2 + 2 = 7 scambi, 2 + 2 = 4 slittamenti. Un discreto miglioramento rispetto al metodo precedente.
In realtà questo algoritmo si dimostra enormemente superiore ai precedenti con un numero elevato di elementi da ordinare.
Questo è il programma che implementa l'algoritmo:
| Shell Sort |
void shellsort(int *a, int n) {
int i, j, temp, incr = n /2;}
while (incr >= 1) {
for (i = incr; i < n; i++)}
temp = a[i];}
j = i;
while (j >= incr && temp < a[j - incr]) {
a[j] = a[j - incr];}
j -= incr;
a[j] = temp;
incr /=2;
Ovviamente, questa strategia di riordinare
preventivamente parti del vettore è applicabile
anche ad altri metodi, con vantaggi veramente elevati
(applicato al Bubble Sort si hanno tempi anche di 100
volte inferiori su un array di 50.000 interi).
Quick Sort
Il Quick Sort è il migliore e più veloce degli algoritmi di sort in quanto sfrutta al meglio la strategia del "divide et impera": visto che la complessità di un ordinamento cresce con il quadrato del numero di elementi, è senz'altro più conveniente riordinare 2 vettori di n / 2 elementi piuttosto che uno solo di n elementi.
Se facciamo un calcolo più preciso, vediamo che il numero dei confronti per ogni ciclo è proporzionale ad n, mentre il numero dei cicli è pari a log2(n).
Infatti questa "strategia" di suddividere in 2 i campi su cui effettuare una ricerca (nel caso che gli elementi siano ordinati) è molto diffusa. Si pensi ad un semplice giochino "alto e basso": bisogna indovinare un numero compreso fra 1 e 100 nel minor numero di tentativi possibile; ad ogni tentativo verrà risposto solo se il numero tentato è più grande o più piccolo di quello da indovinare. La strategia più conveniente è la seguente: prima si tenta con il 50 (media fra 1 e 100), poi, se il numero è troppo piccolo, si tenta con 75 (media fra 51 e 100), e così via. Il campo si restinge prima a 50 numeri, poi a 25, poi a 12, poi a 6, a 3, ed infine ad 1. Con un massimo di 7 tentativi si indovina il numero. È un bel guadagno rispetto ai 100 tentativi che necessari nel caso (sfortunato) si dovessero provare tutti i 100 numeri.
L'algoritmo effettua le seguenti operazioni:
Quick Sort
Il Quick Sort è il migliore e più veloce degli algoritmi di sort in quanto sfrutta al meglio la strategia del "divide et impera": visto che la complessità di un ordinamento cresce con il quadrato del numero di elementi, è senz'altro più conveniente riordinare 2 vettori di n / 2 elementi piuttosto che uno solo di n elementi.
Se facciamo un calcolo più preciso, vediamo che il numero dei confronti per ogni ciclo è proporzionale ad n, mentre il numero dei cicli è pari a log2(n).
Infatti questa "strategia" di suddividere in 2 i campi su cui effettuare una ricerca (nel caso che gli elementi siano ordinati) è molto diffusa. Si pensi ad un semplice giochino "alto e basso": bisogna indovinare un numero compreso fra 1 e 100 nel minor numero di tentativi possibile; ad ogni tentativo verrà risposto solo se il numero tentato è più grande o più piccolo di quello da indovinare. La strategia più conveniente è la seguente: prima si tenta con il 50 (media fra 1 e 100), poi, se il numero è troppo piccolo, si tenta con 75 (media fra 51 e 100), e così via. Il campo si restinge prima a 50 numeri, poi a 25, poi a 12, poi a 6, a 3, ed infine ad 1. Con un massimo di 7 tentativi si indovina il numero. È un bel guadagno rispetto ai 100 tentativi che necessari nel caso (sfortunato) si dovessero provare tutti i 100 numeri.
L'algoritmo effettua le seguenti operazioni:
- si divide il vettore in due parti (partizioni),
non necessariamente uguali, per quanto sarebbe conveniente
che lo fossero, in maniera tale che gli elementi della
prima parte siano tutti più piccoli di quelli
della seconda parte. Eventualmente si effettuano le
operazioni di scambio perché ciò avvenga.
- per meglio suddividere gli elementi in questi due
campi si prende un elemento di confronto (perno o
pivot) che può essere qualsiasi; di solito
si prende l'elemento di mezzo.
- ognuna delle due parti si suddivide in ulteriori
due parti con gli stessi criteri detti in precedenza.
- le operazioni di ordinamento terminano quando ogni
parte non si può suddividere ulteriormente
perché composta di un solo elemento. A questo
punto tutti gli elementi risultano ordinati.
| 5 | 6 | 4 | 3 | 2 | 1 |
L'elemento pivot è il terzo (4).
Nel primo campo prendiamo il primo elemento (a cominciare dal basso) che sia più grande del perno; questo è il 5.
Nel secondo campo prendiamo il primo elemento (a cominciare dall'alto) che sia più piccolo del perno (1).
Scambiamo questi due elementi e avremo:
Nel primo campo prendiamo il primo elemento (a cominciare dal basso) che sia più grande del perno; questo è il 5.
Nel secondo campo prendiamo il primo elemento (a cominciare dall'alto) che sia più piccolo del perno (1).
Scambiamo questi due elementi e avremo:
| 1 | 6 | 4 | 3 | 2 | 5 |
Continuiamo la stessa operazione con
gli elementi successivi (scambiamo 6 e 2):
| 1 | 2 | 4 | 3 | 6 | 5 |
e infine scambiamo 4 e 3:
| 1 | 2 | 3 | 4 | 6 | 5 |
La prima parte risulta già ordinata.
Ora bisogna effettuare l'ordinamento (con lo stesso metodo)
della seconda parte, il vettore:
| 4 | 6 | 5 |
Il nuovo perno è l'elemento di
mezzo (6). Si effettua lo scambio fra 6 e 5 ed abbiamo
anche questo secondo vettore ordinato.
L'implementazione di questo algoritmo è ricorsivo ed data dal seguente programma:
L'implementazione di questo algoritmo è ricorsivo ed data dal seguente programma:
| Quick Sort |
void quicksort(int *a, int in, int en) {
int i, j, k, temp, perno;}
if (in < en) {
i = in;}
j = en;
k = (in + en) / 2;
perno = a[k];
do {
while (a[i] < perno)} while (i <= j);
i++;while (a[j] > perno)
j--;if (i <= j) {
if (a[i] != a[j]) {}
temp = a[i];i++;
a[i] = a[j];
a[j] = temp;
}
j--;
quicksort(a, in, j);
quicksort(a, i, en);
void quicksortp(int *a, int *pend) {
int i, j, temp, perno;}
int *pi, *pj;
if (a < pend) {
pi = a;}
pj = pend;
perno = (*pi + *pend) / 2;
do {
while (*pi < perno)} while (pi <= pj);
pi++;while (*pj > perno)
pj--;if (pi <= pj) {
if (*pi != *pj) {}
temp = *pi;pi++;
*pi = *pj;
*pj = temp;
}
pj--;
quicksortp(a, pj);
quicksortp(pi, pend);
Tabella comparativa
Per un utile confronto, nella tabella che segue si riporta i tempi, in secondi, riscontrati in alcune prove per ordinare 50.000 interi con i vari algoritmi (i tempi dipendono dal computer):
Per un utile confronto, nella tabella che segue si riporta i tempi, in secondi, riscontrati in alcune prove per ordinare 50.000 interi con i vari algoritmi (i tempi dipendono dal computer):
| BubbleSort | 30,00 |
| Bidir-BubbleSort | 23,00 |
| Selection Sort | 13,00 |
| Insertion Sort | 12,00 |
| MergeSort | 9,00 |
| MergeSort (1) | 0,240 |
| BucketSort | 0,050 |
| ShellSort | 0,050 |
| HeapSort | 0,035 |
| QuickSort | 0,031 |
| QuickSort (1) | 0,030 |
| (1) Con ordinamento parziale (2) Versione con puntatori. |
|
Si faccia attenzione che non è lecito generalizzare troppo questi risultati per concludere che un metodo è sempre, ad esempio, il doppio più veloce di un altro e che sia sempre preferibile. Questi tempi dipendono da troppe variabili: il tipo di computer, il linguaggio usato, il numero di elementi e il tipo di array che si sta ordinando e, in qualche caso, potrebbero dare anche indicazioni diverse.
Per un utile confronto riportiamo, nella tabella che segue, i risultati ottenuti sulla stessa macchina e con le stesse funzioni, ma con un numero di elementi di 5.000.000 (100 volte superiore):
| MergeSort (1) | 60,0 |
| BucketSort | 7,5 |
| ShellSort | 15,3 |
| HeapSort | 13,2 |
| QuickSort | 4,1 |
| QuickSort (2) | 3,7 |
| QuickSort (3) | 6,5 |
| (1) Con ordinamento parziale (2) Versione con puntatori. (3) Funzione qsort del C |
|
Non sono stati provati gli algoritmi più lenti che avrebbero richiesto parecchie ore di elaborazione.
MergeSort
Il principio ispiratore del MergeSort è lo stesso del Quick Sort e dello ShellSort, cioè quello di dividere in due parti l'array ed effettuare l'ordinare l'ordinamento su due array più piccoli. Però questo algoritmo non si cura che di spezzare preventivamente il vettore in modo che tutti gli elementi più grandi siano da una parte e quelli più piccoli da un'altra; alla fine del sort i due sottoarray dovranno essere rimessi assieme (merged) con un lavoro non indifferente, che farà aumentare notevolmente il tempo.
Descriviamo l'algortmo con il solito esempio di vettore:
| 4 | 1 | 5 | 6 | 2 | 3 |
Il vettore viene suddiviso in due
parti perfettamente uguali, o quasi, (e questo è
un vantaggio). Avremo quindi i due sotto-array:
|
|
I due sotto-array verranno riordinati
con lo stesso metodo con un procedimento ricorsivo.
Alla fine dell'ordinamento avremo:
|
|
Per fondere assieme i due array in
pratica bisogna effettuare un nuovo ordinamento, ma
preoccupandosi di non alterare il parziale ordine raggiunto
con tanta fatica.
In pratica si confrontano tutti gli elementi del primo array con il primo elemento del secondo array, si scambiano fra loro, se necessario, e si riordinano gli elementi del secondo array.
Nel nostro esempio, prima confrontiamo l'1 con il 2, che restano al loro posto. Poi il 4 viene di nuovo confrontato con il 2 e si scambiano i due elementi. Avremo così:
In pratica si confrontano tutti gli elementi del primo array con il primo elemento del secondo array, si scambiano fra loro, se necessario, e si riordinano gli elementi del secondo array.
Nel nostro esempio, prima confrontiamo l'1 con il 2, che restano al loro posto. Poi il 4 viene di nuovo confrontato con il 2 e si scambiano i due elementi. Avremo così:
|
|
Questo scambio ha alterato l'ordine
del secondo array che dovrà essere di nuovo ordinato,
spostando il 4 nella posizione giusta. Avremo così:
|
|
Infine sarà la volta del 5:
verrà prima scambiato con il 3 e poi spostato
nella giusta posizione
|
|
Questa è la funzione che effettua
il MergeSort:
| Merge Sort |
void mergesort(int *a, int first, int last) {
int i, j, temp, primo;}
int med = (first + last) / 2;
if (first < last) {
mergesort(a, first, med);}
mergesort(a, med + 1, last);
// merge
for (i = first; i <= med; i++) {
primo = a[med + 1];}
if ((temp = a[i]) > primo) {
a[i] = primo;}
for (j = med + 2; j < last && temp > a[j]; j++)
a[j - 1] = a[j];a[j - 1] = temp;
Il punto debole del MergeSort è il lavoro di merge
dei due sottoarray. Un notevole miglioramento si può
avere facendo un preventivo ordinamento parziale, in modo
da spostare gli elementi più grandi in alto e quelli
più piccoli in basso, come nello ShellSort.
Nel listato che segue la funzione msort1 viene richiamata più volte dalla funzione principale mergesort1 per ordinare i sottoarray:
Nel listato che segue la funzione msort1 viene richiamata più volte dalla funzione principale mergesort1 per ordinare i sottoarray:
| Merge Sort 1 |
void msort1(int *a, int first, int last, int incr) {
int i, j, temp, primo, n = (last - first) / incr;}
int med = first + (int)(n / 2) * incr;
if (n > 0) {
msort1(a, first, med, incr);}
msort1(a, med + incr, last, incr);
// merge
for (i = first; i <= med; i += incr) {
primo = a[med + incr];}
if ((temp = a[i]) > primo) {
a[i] = primo;}
for (j = med + 2 * incr; j <= last && temp > a[j]; j += incr)
a[j - incr] = a[j];a[j - incr] = temp;
void mergesort1(int *a, int n) {
int k, incr = n / 2;}
while (incr > 0) {
for (k = 0; k < incr; k++)}
msort1(a, k, n - 1, incr);incr /= 2;
Bucket Sort
Il Bucket Sort è un algoritmo che si presta ad ordinare stringhe di lunghezza fissa ed è particolarmente veloce nel caso nel caso che il numero degli elementi sia molto elevato.
Consiste praticamente nel creare tanti gruppi, quanti sono i caratteri ammessi, in modo che in ciascun gruppo vi siano solo gli elementi che hanno lo stesso carattere nell'ultima posizione. Poi si ripete lo stesso procedimento per il penultimo carattere, il terzultimo, e così via. Al termine avremo l'array ordinato.
Ad esempio, supponiamo di dover ordinare le seguenti stringhe numeriche di 3 cifre:
| 428 | 135 | 056 | 432 | 261 | 426 |
Creiamo 10 contenitori, per lo 0,
per l'1... Poi iniziamo dal primo elemento (428) e lo
mettiamo nel nono contenitore. Passiamo al secondo elemento
(135) e lo mettiamo nel sesto contenitore; il terzo
elemento (056) lo mettiamo nel settimo contenitore e
così via.
Al termine di questo primo ciclo avremo nei vari contenitori, nell'ordine:
Al termine di questo primo ciclo avremo nei vari contenitori, nell'ordine:
| ... | |
| 261 | |
| 432 | |
| ... | |
| ... | |
| 135 | |
| 056 | 426 |
| ... | |
| 428 | |
| ... |
Questi elementi li rimettiamo, nell'ordine,
nell'array che sarà:
| 261 | 432 | 135 | 056 | 426 | 428 |
Rifacciamo la stessa operazione per
in base al secondo elemento e avremo:
| ... | |
| 426 | 428 |
| ... | |
| 432 | 135 |
| ... | |
| 056 | |
| 261 | |
| ... | |
| ... | |
| ... |
Per cui il nuovo vettore sarà:
| 426 | 428 | 432 | 135 | 056 | 261 |
Effettuiamo ora l'ultima operazione
considerando il primo elemento:
| 056 | ||
| 135 | ||
| 261 | ||
| ... | ||
| 426 | 428 | 432 |
| ... | ||
| ... | ||
| ... | ||
| ... | ||
| ... |
Ed abbiamo tutti gli elementi ordinati.
In generale, sono richiesti un numero di cicli pari al numero di caratteri che compongono la stringa (k). Per ogni ciclo sono necessari un numero di confronti pari al numero degli elementi (n). In totale il numero di operazioni è n*k. Quindi, all'aumentare del numero di elementi (se non cambiano il numero di caratteri) il numero di operazioni cresce linearmente.
Ad esempio, per ordinare 50.000 elementi di 5 caratteri ognuno sono necessarie 50.000 * 5 = 250.000 operazioni, contro le 500.000 necessarie per il quick sort o le 2.500.000.000 per il bubble sort. La differenza cresce ancora all'aumentare del numero di elementi.
Per contro, il Bucket Sort richiede molte risorse sul computer. Si pensi che, non sapendo a priori quanti saranno il numero di elementi che confluiranno in ciascun gruppo, dovremo creare per ogni contenitore un array delle stesse dimensioni del vettore da ordinare. Ad esempio, per contenere 100.000 stringhe di 10 caratteri ognuna, sono necessari oltre un milione di byte (100.000 * 11). Saranno poi necessari 26 contenitori, per le 26 lettere dell'alfabeto, di dimensioni analoghe. In totale circa 27 MByte di RAM.
Questo che segue è il listato per l'ordinamento di numeri interi:
In generale, sono richiesti un numero di cicli pari al numero di caratteri che compongono la stringa (k). Per ogni ciclo sono necessari un numero di confronti pari al numero degli elementi (n). In totale il numero di operazioni è n*k. Quindi, all'aumentare del numero di elementi (se non cambiano il numero di caratteri) il numero di operazioni cresce linearmente.
Ad esempio, per ordinare 50.000 elementi di 5 caratteri ognuno sono necessarie 50.000 * 5 = 250.000 operazioni, contro le 500.000 necessarie per il quick sort o le 2.500.000.000 per il bubble sort. La differenza cresce ancora all'aumentare del numero di elementi.
Per contro, il Bucket Sort richiede molte risorse sul computer. Si pensi che, non sapendo a priori quanti saranno il numero di elementi che confluiranno in ciascun gruppo, dovremo creare per ogni contenitore un array delle stesse dimensioni del vettore da ordinare. Ad esempio, per contenere 100.000 stringhe di 10 caratteri ognuna, sono necessari oltre un milione di byte (100.000 * 11). Saranno poi necessari 26 contenitori, per le 26 lettere dell'alfabeto, di dimensioni analoghe. In totale circa 27 MByte di RAM.
Questo che segue è il listato per l'ordinamento di numeri interi:
| Bucket Sort |
void bucketsort(int *a, int n, int nc) {
int i, ii, j, k;}
int *b[10], bn[10];
// crea i 10 contenitori
for (i = 0; i < 10; i++)
b[i] = malloc(sizeof(int) * n);
for (i = 0; i < nc; i++) {
int idiv = (int)pow(10, i);}
int cont;
for (ii = 0; ii < 10; i++)
bn[ii] = 0;for (j = 0; j < n; j++) {
cont = (a[j] / idiv) % 10;}
k = bn[cont];
b[cont][k] = a[j];
bn[cont]++;
k = 0;
for (ii = 0; ii < 10; ii++)
for (j = 0; j < bn[ii]; j++)
a[k++] = b[ii][j];
for (ii = 0; ii < 10; ii++)
free(b[ii]);
La routine viene richiamata con
i seguenti parametri:
HeapSort
L'Heap Sort ricorda il Selection Sort: si seleziona l'elemento più grande e lo si porta in ultima posizione del vettore; poi si trova il più grande degli n - 1 elementi non ordinati e lo si porta in penultima posizione. E così continua fino a che rimane un solo elemento da ordinare.
Ciò che invece contraddistingue questo algoritmo è il metodo per trovare l'elemento più grande. L'array viene pensato strutturato ad albero nella seguente maniera:
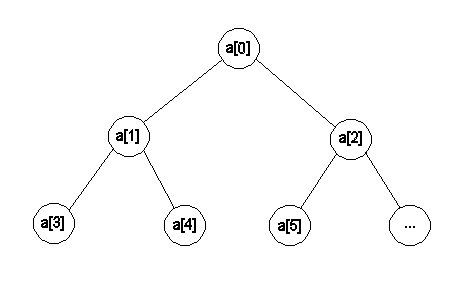
Ad ogni elemento ne sono associati altri due, chiamati figli. I figli di a[0] sono a[1] e a[2]; i figli di a[1] sono a[3] e a[4].
Un array si chiama heap se ogni elemento dell'array è più grande dei figli. Di conseguenza, il primo elemento di un heap è il più grande di tutti gli elementi.
l'Heap Sort consiste, appunto nel trasformare un array in un heap. Al termine di questa operazione il primo elemento, il più grande, viene posto in ultima posizione, scambiandolo con l'ultimo elemento. A questo il problema viene ridotto all'ordinamento di un vettore di n - 1 elementi.
Facciamo un esempio con il seguente vettore:
a: il vettore da ordinare;
n: numero di elementi del vettore;
nc: numero massimo di cifre dei numeri da ordinare.
HeapSort
L'Heap Sort ricorda il Selection Sort: si seleziona l'elemento più grande e lo si porta in ultima posizione del vettore; poi si trova il più grande degli n - 1 elementi non ordinati e lo si porta in penultima posizione. E così continua fino a che rimane un solo elemento da ordinare.
Ciò che invece contraddistingue questo algoritmo è il metodo per trovare l'elemento più grande. L'array viene pensato strutturato ad albero nella seguente maniera:

Ad ogni elemento ne sono associati altri due, chiamati figli. I figli di a[0] sono a[1] e a[2]; i figli di a[1] sono a[3] e a[4].
Un array si chiama heap se ogni elemento dell'array è più grande dei figli. Di conseguenza, il primo elemento di un heap è il più grande di tutti gli elementi.
l'Heap Sort consiste, appunto nel trasformare un array in un heap. Al termine di questa operazione il primo elemento, il più grande, viene posto in ultima posizione, scambiandolo con l'ultimo elemento. A questo il problema viene ridotto all'ordinamento di un vettore di n - 1 elementi.
Facciamo un esempio con il seguente vettore:
| 4 | 1 | 5 | 6 | 2 | 3 |
L'ultimo elemento che ammette figli è il terzo
(numero di elementi diviso 2) per cui cominciamo il
controllo da questo. Il suo unico figlio è
l'ultimo (3). I figli si ottengono moltiplicando la
posizione degli elementi per 2. Siccome 5 è
più grande di 3, questo nodo risulta già
ordinato.
Si passa all'elemento precedente, il secondo, che ha come figli il quarto e il quinto. In questo caso, essendo più piccolo di tutti e due i figli, viene scambiato con il più grande dei due, per cui avremo:
Si passa all'elemento precedente, il secondo, che ha come figli il quarto e il quinto. In questo caso, essendo più piccolo di tutti e due i figli, viene scambiato con il più grande dei due, per cui avremo:
| 4 | 6 | 5 | 1 | 2 | 3 |
Infine si controlla il primo elemento (4) con i suoi
due figli, il secondo e il terzo. Il 4 verrà
scambiato con il 6 e avremo:
| 6 | 4 | 5 | 1 | 2 | 3 |
Il 4 che ha subito lo spostamento in seconda posizione
dovrà essere confrontato con i suoi nuovi figli
(1 e 2) ma non subirà più scambi.
Ora l'array è diventato un heap ed ogni elemento è più grande dei figli. Portiamo il 6 in ultima posizione. Ora rimangono da ordinare solo i primi 5 elementi del vettore, e cioè:
Ora l'array è diventato un heap ed ogni elemento è più grande dei figli. Portiamo il 6 in ultima posizione. Ora rimangono da ordinare solo i primi 5 elementi del vettore, e cioè:
| 3 | 4 | 5 | 1 | 2 |
Bisognerebbe ripetere tutto il procedimento per trasformare
in heap il vettore. Però solo il primo elemento
ha scombinato le cose e non ha figli più piccoli.
Quindi sarà sufficiente riposizionare questo
elemento. Il primo elemento verrà confrontato
con il 4 e il 5 e verrà scambiato con il 5:
| 5 | 4 | 3 | 1 | 2 |
Il 3 in terza posizione non ha figli per cui vettore
è stato trasformato in heap senza ulteriori
passaggi. Il 5, il più grande degli elementi
verrà scambiato con il 2 e l'ordinamento continua
con:
| 2 | 4 | 3 | 1 |
Per trasformarlo in heap il 2 verrà scambiato
con il primo figlio (4):
| 4 | 2 | 3 | 1 |
Il 4 viene scambiato con l'elemento in ultima posizione
e l'ordinamento continua con:
| 1 | 2 | 3 |
Il vettore risulta già ordinato, però
il procedimento obbliga a trasformarlo prima in heap
(scambiando l'1 con il 3) e poi a spostare il 3 in
ultima posizione, scambiandolo di nuovo con l'1. La
stessa cosa succede per il successivo passo, nell'ordinare
il vettore di 2 elementi composto da 1 e da 2 che
verranno scambiati fra loro per due volte. In ogni
caso, a questo punto avremo il vettore ordinato.
Il seguente modulo mostra i vari passaggi dell'Heap Sort:
Il seguente modulo mostra i vari passaggi dell'Heap Sort:
Scriviamo il programma che effettua l'HeapSort.
Anzitutto si costruisce la funzione che trasforma
il vettore in heap. I parametri richiesti da questa
funzione, oltre al vettore da ordinare, sono il
nodo k (l'elemento che deve essere confrontato con
i figli) e il la dimensione del vettore.
void downHeap(int *a, int k, int n) {
int elem, child;}
elem = a[k];
while (k < n / 2) {
child = 2 * k + 1;}
if (child < n - 1 && a[child] < a[child + 1])
child+;if (elem > a[child])
break;a[k] = a[child];
k = child;
a[k] = elem;
La funzione che effettua il sort è:
| Heap Sort |
void heapSort(int *a, int n) {
int i, temp;}
// trasforma in heap il vettore
for (i = n - 1; i > 0; i--)
downHeap(a, i, n);
for (i = n; i > 0; i--) {
// scambia il primo con l'ultimo}
temp = a[i];
a[i] = a[0];
a[0] = temp;
// rimetti a posto il vettore
downHeap(a, 0, i);