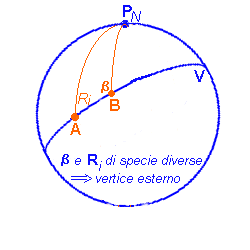
Una circonferenza massima divide la sfera in due parti perfettamente uguali, dette emisferi. L'ortodromia si sviluppa per metà nell'emisfero Nord e per metà in quello Sud.

Sulla superficie di una sfera, per ogni coppia A, B di punti ( che non siano agli antipodi) passa una e una sola circonferenza massima. Questo perché per 3 punti non allineati (A, B e O centro della sfera) passa uno ed un solo piano che determina una sola circonferenza massima.

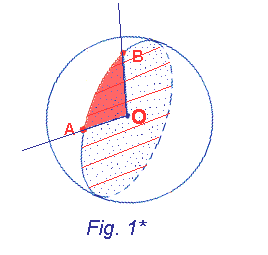
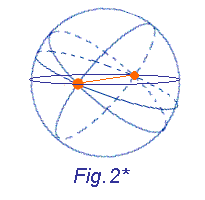
Invece per due punti agli antipodi passano infinite circonferenze massime (vedi Fig. 2*).

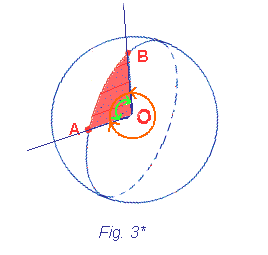
Due punti qualsiasi A e B divideranno l'ortodromia in due archi di circonferenza massima: AB e BA. Ad ognuno di essi corrisponderà un rispettivo angolo al centro. L'arco di circonferenza massima sotteso ad un angolo minore di 180° rappresenterà la minima distanza tra i 2 punti. Infatti se sul piano, il percorso più breve è il segmento che unisce i 2 punti, essendo l'ortodromia ricavata dal piano che taglia la sfera, la distanza più breve è l'arco di circonferenza massima passante per i 2 punti. Questo è il principale vantaggio della navigazione ortodromica.

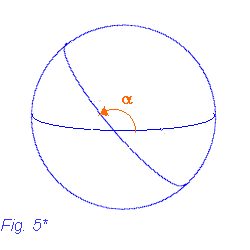
E' evidente (vedi Fig. 4*), nonchè dimostrabile, che un'ortodromia incontra i meridiani sotto angoli variabili. Pertanto per seguire il percorso più breve tra due punti dovremo cambiare continuamente rotta.

Infatti in figura si vede chiaramente che

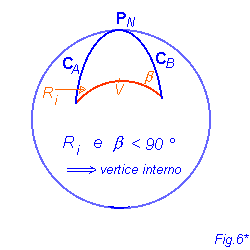
Ri Rf

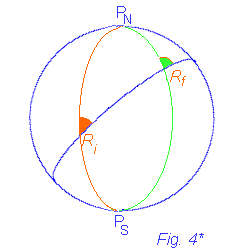
Oltre ad essere evidente dal grafico ciò è dimostrabile con opportuni teoremi di trigonometria sferica (pentagono di Nepero). Questo è un grosso svantaggio della navigazione ortodromica.

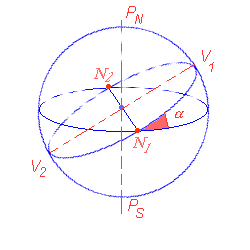
Un'ortodromia ha due punti più alti in latitudine che chiameremo vertici (V1 e V2 nella Fig. 5*) diametralmente opposti, e agli antipodi.

Un' ortodromia incontra l'equatore in due punti diametralmente opposti, N1 e N2, agli antipodi l'uno dell' altro, detti nodi. Per convenzione il nodo principale è quello che si trova nell'emisfero Est. Nel caso in Fig. 5* quindi è N1 il nodo principale.

Ogni ortodromia viene individuata univocamente dalla longitudine del nodo principale l_N e dall'angolo a che forma con l'equatore. Equazione caratteristica dell'ortodromia è:

tg j = sen ( l - l_N ) tg a

Un'ortodromia incontra un parallelo in due punti simmetrici rispetto al vertice.

I vertici consentono direttamente il calcolo di l_N ed a. Infatti, essendo i vertici diametralmente opposti, si capisce che:

se a < 90°	risulta che
mentre se a > 90°	risulta che

Se, tanto per fissare le idee, fosse a = 45°, allora le latitudini dei due vertici sarebbero j_V1 =45° N; e j_V2 = 45° S.

Per la simmetria sferica dell'ortodromia, si dimostra che tra i vertici ed i nodi esiste una differenza di longitudine di 90°. Cioè:

Il vertice dell'ortodromia forma con il meridiano un angolo di 90°. Anche questo è dimostrabile con opportuni teoremi di trigonometria sferica (pentagono di Nepero).

Un vertice può cadere all'interno o all'esterno del percorso ortodromico AB. Cadrà all'interno quando i due angoli (Ri e b) sono della stessa specie, cioè entrambi minori di 90°, cadrà all'esterno quando i due angoli (Ri e b) saranno di specie diverse, uno minore di 90° e uno maggiore di 90° (vedi fig.6* ).

L'ortodromia, a differenza della lossodromia, non presenta punti di flesso sulla terra (cioè non cambia di concavità).