Applicazione dei teoremi studiati

Quesito B proposto agli Esami di Stato 2001/2002
TESTO
Un aeromobile parte dalla base di Guantanamo(Lat. = 20° 00' N, long. = 75° 00' W) diretto al waypoint B (Lat. = 40° 00' N, Long. =50° 00' W) seguendo l'ortodromia.
Il candidato determini le coordinate del punto in cui l'aeromobile si troverą pił vicino al centro ATS delle Bermude (Lat. = 32° 20' N, Long. =64° 45' W) e la relativa distanza.

Soluzione
Guantanamo, spesso protagonista della politica internazionale, è una base americana situata a Sud dell'isola di CUBA.

Costruiamo la scena:

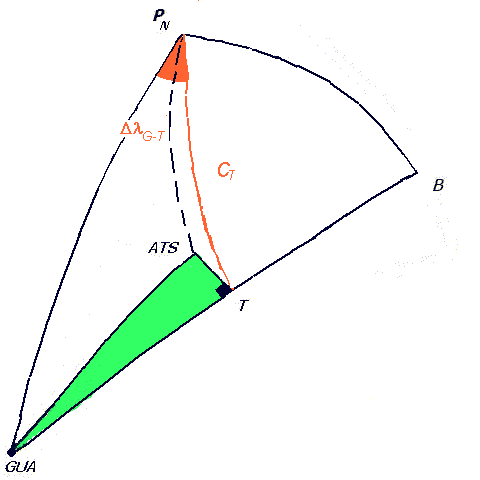
Diciamo T il punto da individuare.

Determinare le coordinate del punto T si traduce nel determinare DlG-T e CT e quindi servirà raccogliere più informazioni possibili sul triangolo sferico GUA - PN - T.

Si osservi che il triangolo sferico GUA - ATS - T è rettangolo dovendo essere T il punto più vicino al centro ATS.

 
Operazioni sul triangolo sferico GUA - PN - B

Tenendo conto che: Dl GUA-B = 25° E, calcoliamo la distanza dGUA- B con il Teorema di Eulero:

cos dG - B = sen jG senjB+ cosjG cos jB cosDl


cos dG - B = sen20°sen40°+ cos20°cos40°cos25° =0,87

dG - B = 29° 16' 44'' = 1756.74 NM

Calcolo di Ri con la regola di Vieta:

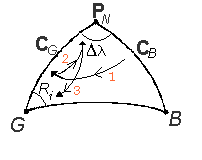
ctgCB senCG = cosCG cosDl + sen Dl ctgRi

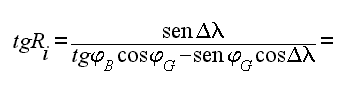
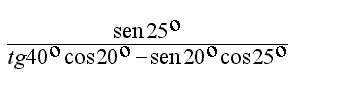
Ne segue che Ri = N 41° 27' E = 41° 27'

(N.B. qui si prescinde dai segni poichè entrambi i punti sono nell'emisfero Nord e le convenzioni sul triangolo sferico si sposano perfettamente con quelle di navigazione)

 
Operazioni sul triangolo sferico GUA - PN - ATS

Intanto è Dl GUA- ATS = 64°45' W - 75° W = 10°15' E

Calcolo di dG - ATS con il Teorema di Eulero

cosdG - ATS = sen20° sen32°20' + cos 20° cos32°20' cos10°15' = 15°22' = 922 NM

ed anche qui calcolo Ri con la regola di Vieta

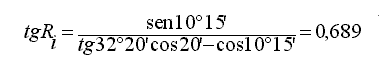
Ri = N 34.56 E = 34° 34'

(N.B. anche qui si prescinde dai segni poichè entrambi i punti sono nell'emisfero Nord)

Operazioni sul triangolo rettangolo GUA - ATS - T

Questo triangolo è rettangolo per ipotesi e risulta:

DRi = 41°27' - 34°34' = 6°53'

Applichiamo la regola mnemonica di Nepero:

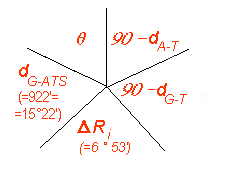
cosDRi =ctg dG-A ctg(90° - dG-T)

quindi: cos(6° 53') = cgt(15°22') tgdG-T

tgdG-T = cos(6° 53') tg(15°22') = cos(6° 53') tg(15° 22') = 0,27

da cui segue che dG-T = 15° 15' 39'' = 915,6 NM

Operazioni sul triangolo sferico GUA - PN - T

Applichiamo il Teorema di Eulero per determinare la colatitudine di T:

cosCT = cos CG cosdG-T + senCG sendG-T cosRi

cosCT = cos(90°- jG) cos(915,6') + sen(90°- jG) sen(915,6') cos(41° 27')

cos(90°- jT) = sen jG cos(15° 15' 39'') + cosjG sen(15° 15' 39'') cos(41° 27')

senjT = sen20° cos(15° 15' 39'') + cos 20° sen(15° 15' 39'') cos(41° 27')

jT = 31° 1' 15'' N

Applichiamo sempre il Teorema di Eulero per il calcolo di Dl:

cosdG-T = cosCG cosCT + senCG senCT cosDl

cosdG-T = senjG senjT + cosjG cosjT cosDl

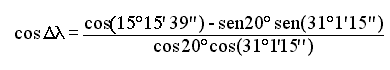
Dl = 11° 43' 52'' E

[ lT = lG + Dl = 75° - 11° 43' 52'' = 63° 16' W ]

Torna ai quesiti del 2002