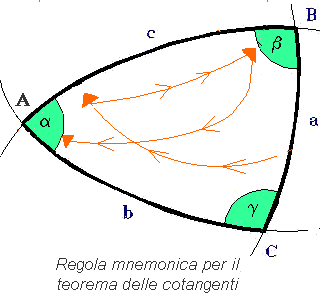
La Regola empirica di Vieta o formula delle cotangenti

Si tratta di una formula che lega fra loro quattro elementi consecutivi di un triangolo sferico: due lati e due angoli. Riferendoci al triangolo sferico classico ABC indicato in figura, siano a, b, c, a i quattro elementi consecutivi da legare tra loro. All'interno del triangolo si traccia una linea spezzata come mostrato in figura, si parte dal lato a (lato non compreso fra i due angoli), si va all'altro lato c, si ritorna nell'angolo compreso b e si raggiunge infine l'angolo a opposto al lato a di partenza.

Si scrivono due terne di funzioni, di cui la prima è Ctg, Sin e Cos (cotangente, seno e coseno) e la seconda è l’immagine speculare della prima; le sei funzioni trigonometriche vanno divise in tre coppie, fra la prima e la seconda si pone il segno d'uguaglianza, fra le ultime due si pone il segno più.
Gli argomenti delle sei funzioni trigonometriche sono nell'ordine quelli indicati dalla precedente spezzata, con l'avvertenza di scrivere due volte gli elementi corrispondenti alle cuspidi della spezzata: angolo b e lato c nell'esempio di figura. Nell’esempio proposto si ha in definitiva:

Ctg a Sen b = Cos b Cos g + Sen g Ctg a
Ctg b Sen a = Cos a Cos g + Sen g Ctg b
Ctg b Sen c = Cos c Cos a + Sen a Ctg b
Ctg c Sen a = Cos a Cos b + Sen b Ctg g
Ctg c Sen b = Cos b Cos a + Sen a Ctg g

Si ricorda che la regola di VIETA, valida matematicamente, può perdere di validità nelle applicazioni di navigazione, in quanto le convenzioni sugli angoli si scontrano con le convenzioni che attribuiscono al Nord e all'Est il segno " più + " e al Sud e all'Ovest il segno" meno - ".

Torna alla pagina precedente