CALCOLO COMBINATORIO
![]()
Quel ramo della matematica che si occupa di contare in quanti modi è possibile raggruppare gli elementi di un insieme, si chiama calcolo combinatorio.
Se volessimo determinare la probabilità che esca un certo ambo al gioco del lotto, si tratterebbe di vedere prima quanti ambi si possono realizzare con i numeri del lotto (per individuare il numero dei casi possibili).
Quando, nel contare il numero di raggruppamenti diversi è importante l’ordine, di parla di DISPOSIZIONI . se l’ordine non riveste importanza si parla invece di COMBINAZIONI .
DISPOSIZIONI
Si chiamano disposizioni di n elementi presi a k a k tutti i gruppi che si possono costruire con k degli n elementi dati, in modo che ogni gruppo differisca dall’altro o per qualche elemento o per l’ordine secondo cui gli elementi sono disposti. Il numero delle disposizioni di n elementi a k a k è uguale al prodotto di k numeri interi consecutivi decrescenti di cui il primo è n:
D
n,k = n (n-1) (n-2) ……….(n-k+2) (n-k+1)ESEMPIO
Su una panchina possono sedere contemporaneamente soltanto 4 persone, in quanti modi 10 amici possono formare un gruppo che occupi tale panchina?
D
10,4 = 10 · 9 · 8 · 7 = 5.040
PERMUTAZIONI
Si chiama permutazione di n oggetti distinti una qualsiasi disposizione di n oggetti, presi n ad n.
P
n = n! = n (n-1) (n-2) · · 3 · 2 · 1ESEMPIO
Un tale deve appendere 6 quadri, allineandoli sulla stessa parete. In quanti modi diversi può farlo?
P
6 = 6 · 5· 4 · 3· 2· 1 = 720COMBINAZIONI
Si chiamano combinazioni di n elementi presi a k a k tutti i gruppi che si possono formare con k degli n elementi dati, considerando distinti quei gruppi che differiscono soltanto per qualche elemento. Si dimostra che le combinazioni semplici (senza ripetizioni) di n elementi presi k a k è dato da:
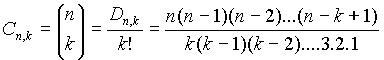
ESEMPIO
Qual è il numero di tutte le cinquine che possono uscire sulla ruota di Milano?
Le combinazioni di 90 elementi presi a 5 a 5:
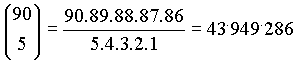
ESERCIZIO 1
In quanti modi è possibile scegliere, all’interno di una classe di 25 alunni, i due rappresentanti di classe?
Il numero delle coppie di alunni che si possono ottenere con 25, poiché in ogni coppia non è importante l’ordine dei ragazzi che la costituiscono, è dato dal numero delle combinazioni semplici che si ottengono con 25 elementi presi 2 a 2, quindi:
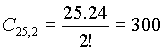
ESERCIZIO 2
Fra tutte le possibili parole ottenute anagrammando la parola GRANO, qual è la probabilità di ottenere la parola RAGNO? Tutti i possibili anagrammi della parola grano sono le permutazioni di 5 elementi, cioè 120 e formano la totalità dei casi possibili. L’evento favorevole è 1, quindi la probabilità è 1/120.
![]()
clicca qui per tornare ad "eventi"

clicca qui per tornare alla pagina di MATEMATICA
![]()
![]()
![]()
![]()
![]()
![]()