L'Integrazione approssimata
(di Maurizio Mauri)
(di Maurizio Mauri)
L'integrazione
numerica (chiamata anche quadratura) permette di determinare un valore
approssimato dell'integrale definito.
Ricordiamo che l'integrale definito di una funzione y = f(x) rappresenta geometricamente l'area sottesa dalla funzione rispetto all'ascissa.
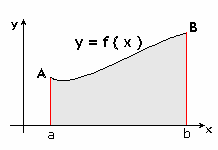
I metodi numerici per il calcolo dell'integrale approssimano la forma dell'area da calcolare ad una più semplice.
Metodo del punto centrale.
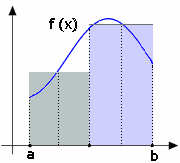 L'area da calcolare viene approssimata a quella di un rettangolo con base
l'ampiezza dell'intervallo e come altezza il valore che la funzione assume
nel punto di mezzo.
L'area da calcolare viene approssimata a quella di un rettangolo con base
l'ampiezza dell'intervallo e come altezza il valore che la funzione assume
nel punto di mezzo.
Indicato con xM l'ascissa del punto di mezzo, pari a (a + b) / 2, l'area viene approssimata a:
A = (b - a) f(xM);
È evidente che l'errore commesso è molto elevato. Per migliorare la precisione dividiamo l'intervallo (a, b) in tanti intervalli. L'integrale viene calcolato come somma delle aree dei rettangoli definiti in questa maniera. Se scegliamo n intervalli della stessa ampiezza, valgono le formule:
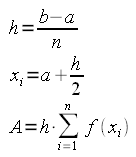
Tanto più elevato è il numero degli intervalli tanto più preciso è il risultato.
Come esempio prendiamo la funzione y = cos(x) e calcoliamo l'integrale fra 0 e π/2. In questo caso possiamo determinare analiticamente possiamo il risultato preciso, che potrà essere confrontato con il valore approssimato.
Infatti I = sin(π/2) - sin(0) = 1
Facciamo il calcolo approssimato tramite alcune funzioni javascript. Definiamo, anzitutto la funzione:
La funzione che calcola l'area di n intervalli può essere la seguente:
// n : numero di intervalli
// a e b : estremi dell'intervallo
function midpoint(n, a, b) {
Calcoliamo ora il valore suddividendo in 10 intervalli:
riporta un risultato abbastanza preciso:
con un errore di circa 1 per mille.
Vediamo ora come si evolve l'errore suddividendo l'intervallo (a, b) in intervalli sempre più fitti:
Si noti come moltiplicando il numero di intervalli per 10, l'errore diventa 100 volte più piccolo.
Metodo dei trapezi.
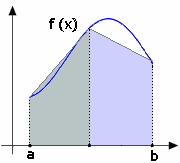 L'area viene approssimata ad un trapezio avente come basi i valori che
la funzione assume agli estremi dell'intervallo e come altezza l'ampiezza
dell'intervallo:
L'area viene approssimata ad un trapezio avente come basi i valori che
la funzione assume agli estremi dell'intervallo e come altezza l'ampiezza
dell'intervallo:
A = (b - a)(f(a) + f(b)) / 2
Suddividendo in n intervalli, l'integrale viene calcolato come somma delle aree dei trapezi.
Suddividiamo, all'inizio in due intervalli uguali, con estremi x0, x1, x2. Le due aree valgono rispettivamente:
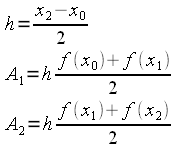
Sommando si ha:
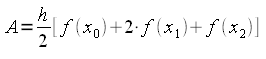
Generalizzando, per n intervalli della stessa ampiezza possiamo scrivere:
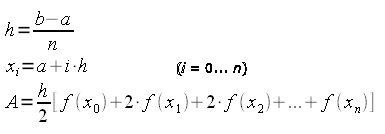
Costruiamo la funzione per il calcolo:
Calcoliamo l'integrale per diversi intervalli (10, 100, 1000) con questi risultati:
Come si vede l'errore è confrontabile con quello del precedente metodo e decresce nella stessa maniera all'aumentare degli intervalli.
Metodo di Cavalieri-Simpson
Con questo metodo il numero di intervalli n deve essere per forza pari. Questi intervalli, presi due alla volta, definiscono tre punti per i quali si considera la parabola che vi passa.
Sommando tutti questi contributi si arriva alla formula:
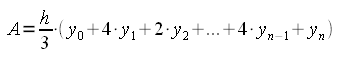
Questo č la funzione che permette di calcolare l'integrale: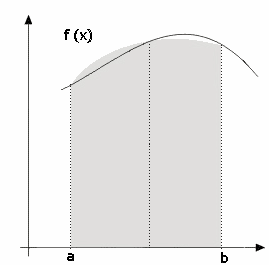
Questo è l'output del programma per un numero di intervalli pari a 1, 10, 100 e 1000:
Si noti la maggiore precisione del metodo. Con soli 10 intervalli si ottiene la precisione che con i precedenti metodi si otteneva con un numero di intervalli superiore a 100.
Si noti inoltre come, moltiplicando per 10 il numero di intervalli si ottiene una precisione 10000 volte maggiore.
Metodo di Romberg
Il metodo di Romberg consiste nell'applicazione dell'estrapolazione di Richardson al metodo dei trapezi.
Si è parlato brevemente sull'estrapolazione di Richardson quando si è illustrato il calcolo approssimato della derivata. Qui verrà soltanto mostrata la sua applicazione al metodo dei trapezi.
Si calcolano, anzitutto, due valori dell'integrale con il metodo dei trapezi. Il primo valore viene calcolato con un solo intervallo; il valore successivo per un numero doppio di intervalli. Questi due valori verranno indicati con R[0][0] e R[1][0].
Nel nostro caso (con la funzione y = cos(x) che abbiamo scelto come esmpio) otteniamo rispettivamente:
Questi due valori permettono di ricavare un altro valore pių preciso tramite la seguente formula (estrapolazione di Richardson):
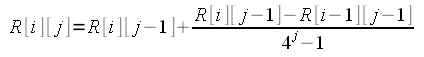
In cui i e j valgono, in questo caso, 1 e 0. Il nuovo valore (R[1][1]) vale 1.0022798774922104 con un errore (differenza fra gli ultimi due valori calcolati, R[1][1] e R[1][0], in valore assoluto) di 0.05422042852369047.
Poiché l'errore è troppo elevato si deve suddividere ulteriormente (si dimezza) l'intervallo. Quindi si provede a calcolare il valore fornito dal metodo dei trapezi per n = 4. Il nuovo valore (R[2][0]) risulta 0.9871158009727754. Si calcola, con la formula di Richardson il valore successivo (R[2][1]) pari a 1.0001345849741938 con un errore evidentemente più piccolo. Estrapolando ulteriormente questo valore con quello ottenuto in precedenza otteniamo R[2][2] = 0.9999915654729927 il cui errore è (R[2][2] - R[1][1] in valore assoluto) 0.00014301950120110263.
In sintesi abbiamo ottenuto la seguente matrice triangolare:
in cui, da due valori contigui della prima colonna abbiamo ottenuto dei valore della seconda colonna. Da questi ne abbiamo ottenuto un ultimo della terza colonna. Le celle con sfondo grigio rappresentano l'errore.
Ovviamente possiamo continuare il calcolo raddoppiando ancora il numero degli intervalli. Con n = 5 (5 valori ottenuti con il metodo dei trapezi) abbiamo il seguente risultato:
Si tenga presente che con un prefissato valore di n si arriva a suddivedere in 2n - 1 intervalli (16 nel caso precedente). Con soli 16 intervalli otteniamo risultati della stessa precisione che si ottiene col metodo di Cavalieri-Simpon con un numero ben superiore di intervalli (1000).
Con il metodo di Romberg è possibile, inoltre, controllare l'errore. Si può interrompere il calcolo appena è stata raggiunta la precisione desiderata. Deve, in ogni caso, essere vissato il numero massimo di suddivisioni poiché in base a questo numero viene dimensionato l'array che contiene i valori da estrapolare.
Si riporta il listato per il calcolo dell'integrale con il metodo di Romberg:
Si faccia caso alle istruzioni:
Queste permettono di richiamare la funzione romberg con un quarto parametro (opzionale) che rappresenta la funzione da integrare. In mancanza di questo parametro viene integrata la funzione definita in precedenza f(x)
Calcolo di PI greco
Come ulteriore esempio utilizziamo il metodo di Romberg per il calcolo di alcune cifre di PI greco.
Si ricorda che π è un numero irrazionale trascendente (infinite cifre decimali non periodiche) definito come il rapporto fra una circonferenza e il suo diametro. Il calcolo delle cifre di questo numero, noto sin dall'antichità, ha sempre affascinato i matematici che hanno sviluppato molti metodo di calcolo. Lo stesso Newton, nella sua famosa "primavera", si divertiva a calcolare qualche cifra decimale di π (16).
Per il nostro calcolo terremo conto che:
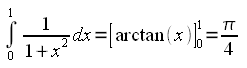
Quindi π viene calcolato con la formula:
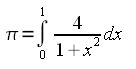
Per il calcolo è sufficiente richiamare la funzione romberg nella seguente maniera:
che produce questo risultato:
Nota: per la stampa formattata viene usata la funzione printf() che non è una funzione standard del javascript; essa è contenuta in una apposita utility.
Ricordiamo che l'integrale definito di una funzione y = f(x) rappresenta geometricamente l'area sottesa dalla funzione rispetto all'ascissa.
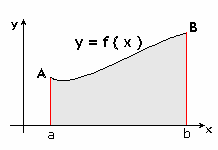
I metodi numerici per il calcolo dell'integrale approssimano la forma dell'area da calcolare ad una più semplice.
Metodo del punto centrale.

Indicato con xM l'ascissa del punto di mezzo, pari a (a + b) / 2, l'area viene approssimata a:
A = (b - a) f(xM);
È evidente che l'errore commesso è molto elevato. Per migliorare la precisione dividiamo l'intervallo (a, b) in tanti intervalli. L'integrale viene calcolato come somma delle aree dei rettangoli definiti in questa maniera. Se scegliamo n intervalli della stessa ampiezza, valgono le formule:
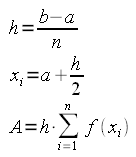
Tanto più elevato è il numero degli intervalli tanto più preciso è il risultato.
Come esempio prendiamo la funzione y = cos(x) e calcoliamo l'integrale fra 0 e π/2. In questo caso possiamo determinare analiticamente possiamo il risultato preciso, che potrà essere confrontato con il valore approssimato.
Infatti I = sin(π/2) - sin(0) = 1
Facciamo il calcolo approssimato tramite alcune funzioni javascript. Definiamo, anzitutto la funzione:
function f(x) {
return Math.cos(x);
}
return Math.cos(x);
}
La funzione che calcola l'area di n intervalli può essere la seguente:
// n : numero di intervalli
// a e b : estremi dell'intervallo
function midpoint(n, a, b) {
var h = (b - a) / n;
var i;
var x = a + h / 2;
var s = 0;
for (i = 0; i < n; i++) {
return s * h;
}var i;
var x = a + h / 2;
var s = 0;
for (i = 0; i < n; i++) {
s += f(x);
x += h;
}x += h;
return s * h;
var n = 10;
document.write("Integrale(" + n + ") = " + midpoint(n, 0, Math.PI / 2));
document.write("Integrale(" + n + ") = " + midpoint(n, 0, Math.PI / 2));
riporta un risultato abbastanza preciso:
1.0010288241427083
con un errore di circa 1 per mille.
Vediamo ora come si evolve l'errore suddividendo l'intervallo (a, b) in intervalli sempre più fitti:
Si noti come moltiplicando il numero di intervalli per 10, l'errore diventa 100 volte più piccolo.
Metodo dei trapezi.

A = (b - a)(f(a) + f(b)) / 2
Suddividendo in n intervalli, l'integrale viene calcolato come somma delle aree dei trapezi.
Suddividiamo, all'inizio in due intervalli uguali, con estremi x0, x1, x2. Le due aree valgono rispettivamente:
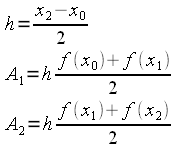
Sommando si ha:
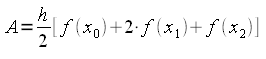
Generalizzando, per n intervalli della stessa ampiezza possiamo scrivere:
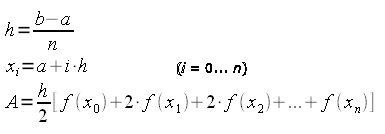
Costruiamo la funzione per il calcolo:
function trapezi(n, a, b) {
var h = (b - a) / n;
var i;
var x = a + h;
var s = f(a) + f(b);
for (i = 1; i < n; i++) {
return s * h / 2;
}var i;
var x = a + h;
var s = f(a) + f(b);
for (i = 1; i < n; i++) {
s += 2 * f(x);
x += h;
}x += h;
return s * h / 2;
Calcoliamo l'integrale per diversi intervalli (10, 100, 1000) con questi risultati:
Come si vede l'errore è confrontabile con quello del precedente metodo e decresce nella stessa maniera all'aumentare degli intervalli.
Metodo di Cavalieri-Simpson
Con questo metodo il numero di intervalli n deve essere per forza pari. Questi intervalli, presi due alla volta, definiscono tre punti per i quali si considera la parabola che vi passa.
Sommando tutti questi contributi si arriva alla formula:
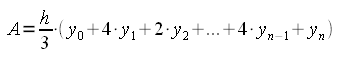
Questo č la funzione che permette di calcolare l'integrale:

function simpson(n, a, b){
if (n % 2 != 0) n++;
var h = (b - a) / n;
var s = f(a) + f(b);
var i;
var fg = true;
var x = h;
var c;
for (i = 1; i < n; i++) {
return s * h/3;
}var h = (b - a) / n;
var s = f(a) + f(b);
var i;
var fg = true;
var x = h;
var c;
for (i = 1; i < n; i++) {
c = fg ? 4 : 2;
s += c * f(x);
x += h;
fg = !fg;
}s += c * f(x);
x += h;
fg = !fg;
return s * h/3;
Questo è l'output del programma per un numero di intervalli pari a 1, 10, 100 e 1000:
Si noti la maggiore precisione del metodo. Con soli 10 intervalli si ottiene la precisione che con i precedenti metodi si otteneva con un numero di intervalli superiore a 100.
Si noti inoltre come, moltiplicando per 10 il numero di intervalli si ottiene una precisione 10000 volte maggiore.
Metodo di Romberg
Il metodo di Romberg consiste nell'applicazione dell'estrapolazione di Richardson al metodo dei trapezi.
Si è parlato brevemente sull'estrapolazione di Richardson quando si è illustrato il calcolo approssimato della derivata. Qui verrà soltanto mostrata la sua applicazione al metodo dei trapezi.
Si calcolano, anzitutto, due valori dell'integrale con il metodo dei trapezi. Il primo valore viene calcolato con un solo intervallo; il valore successivo per un numero doppio di intervalli. Questi due valori verranno indicati con R[0][0] e R[1][0].
Nel nostro caso (con la funzione y = cos(x) che abbiamo scelto come esmpio) otteniamo rispettivamente:
R[0][0] = 0.7853981633974483
R[1][0] = 0.9480594489685199
R[1][0] = 0.9480594489685199
Questi due valori permettono di ricavare un altro valore pių preciso tramite la seguente formula (estrapolazione di Richardson):
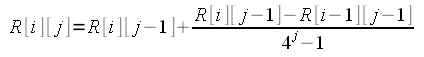
In cui i e j valgono, in questo caso, 1 e 0. Il nuovo valore (R[1][1]) vale 1.0022798774922104 con un errore (differenza fra gli ultimi due valori calcolati, R[1][1] e R[1][0], in valore assoluto) di 0.05422042852369047.
Poiché l'errore è troppo elevato si deve suddividere ulteriormente (si dimezza) l'intervallo. Quindi si provede a calcolare il valore fornito dal metodo dei trapezi per n = 4. Il nuovo valore (R[2][0]) risulta 0.9871158009727754. Si calcola, con la formula di Richardson il valore successivo (R[2][1]) pari a 1.0001345849741938 con un errore evidentemente più piccolo. Estrapolando ulteriormente questo valore con quello ottenuto in precedenza otteniamo R[2][2] = 0.9999915654729927 il cui errore è (R[2][2] - R[1][1] in valore assoluto) 0.00014301950120110263.
In sintesi abbiamo ottenuto la seguente matrice triangolare:
in cui, da due valori contigui della prima colonna abbiamo ottenuto dei valore della seconda colonna. Da questi ne abbiamo ottenuto un ultimo della terza colonna. Le celle con sfondo grigio rappresentano l'errore.
Ovviamente possiamo continuare il calcolo raddoppiando ancora il numero degli intervalli. Con n = 5 (5 valori ottenuti con il metodo dei trapezi) abbiamo il seguente risultato:
Si tenga presente che con un prefissato valore di n si arriva a suddivedere in 2n - 1 intervalli (16 nel caso precedente). Con soli 16 intervalli otteniamo risultati della stessa precisione che si ottiene col metodo di Cavalieri-Simpon con un numero ben superiore di intervalli (1000).
Con il metodo di Romberg è possibile, inoltre, controllare l'errore. Si può interrompere il calcolo appena è stata raggiunta la precisione desiderata. Deve, in ogni caso, essere vissato il numero massimo di suddivisioni poiché in base a questo numero viene dimensionato l'array che contiene i valori da estrapolare.
Si riporta il listato per il calcolo dell'integrale con il metodo di Romberg:
function romberg(n, a, b) {
if (arguments.length
> 3)
var i;
for (i = 0; i < n; i++)
var eps = 1e-15, eps1;
i = 1;
while (i < n) {
return R[i][i];
}fx = arguments[3];
else
fx = f;
var R = new Array();var i;
for (i = 0; i < n; i++)
R[i] = new Array();
R[0][0] = (b - a) / 2 * (fx(a) + fx(b));var eps = 1e-15, eps1;
i = 1;
while (i < n) {
var nx = Math.pow(2, i);
var h = (b - a) / nx;
var s = 0;
for (var k = 0; k < Math.pow(2, i - 1); k++) {
R[i][0] = 0.5 * R[i - 1][0] + h * s;
for (var j = 1; j < i + 1; j++)
if (eps1 < eps || i == n - 1)
}var h = (b - a) / nx;
var s = 0;
for (var k = 0; k < Math.pow(2, i - 1); k++) {
var xx = a +
(2 * k + 1) * h;
s += fx(xx);
}s += fx(xx);
R[i][0] = 0.5 * R[i - 1][0] + h * s;
for (var j = 1; j < i + 1; j++)
R[i][j] = R[i][j - 1] + (R[i][j - 1] - R[i - 1][j - 1]) / (Math.pow(4, j) - 1);
eps1 = Math.abs(R[i][i - 1] - R[i][i]);if (eps1 < eps || i == n - 1)
break;
i++;return R[i][i];
Si faccia caso alle istruzioni:
if (arguments.length > 3)
fx = arguments[3];
Queste permettono di richiamare la funzione romberg con un quarto parametro (opzionale) che rappresenta la funzione da integrare. In mancanza di questo parametro viene integrata la funzione definita in precedenza f(x)
Calcolo di PI greco
Come ulteriore esempio utilizziamo il metodo di Romberg per il calcolo di alcune cifre di PI greco.
Si ricorda che π è un numero irrazionale trascendente (infinite cifre decimali non periodiche) definito come il rapporto fra una circonferenza e il suo diametro. Il calcolo delle cifre di questo numero, noto sin dall'antichità, ha sempre affascinato i matematici che hanno sviluppato molti metodo di calcolo. Lo stesso Newton, nella sua famosa "primavera", si divertiva a calcolare qualche cifra decimale di π (16).
Per il nostro calcolo terremo conto che:
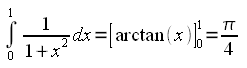
Quindi π viene calcolato con la formula:
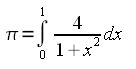
Per il calcolo è sufficiente richiamare la funzione romberg nella seguente maniera:
romberg(6, 0, 1, new Function("x", "return 4 / (1 + x *
x)"));
che produce questo risultato:
---------------
Nota: per la stampa formattata viene usata la funzione printf() che non è una funzione standard del javascript; essa è contenuta in una apposita utility.