SOLUZIONI SCHEDA n.6

Si dice che la curva g , di equazione y = f (x) ammette la retta r come asintoto se:

la distanza del generico punto P della curva dalla retta r tende a zero quando P si allontana indefinitamente su g .

nel qual caso il suddetto asintoto ha equazione: à x = c

nel qual caso il suddetto asintoto ha equazione: à y = l

La curva di equazione y = f (x) presenta un asintoto obliquo se esistono entrambi i limiti: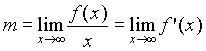

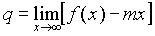
nel qual caso il suddetto asintoto ha equazione: y = mx + q

Una funzione razionale frazionaria ammette asintoto obliquo se e solo se il grado del numeratore supera di un'unità il grado del denominatore, nel qual caso l'equazione dell'asintoto si trova facendo il quoziente della divisione del numeratore per il denominatore.

 Per quanto riguarda la curva nel grafico 

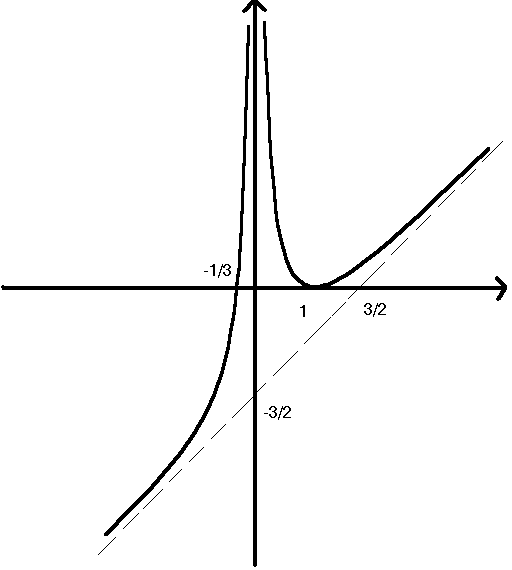
Insieme di definizione: x ¹ 0

Asintoto obliquo di equazione: y = x - 3/2

Asintoto verticale di equazione: x = 0

Passa per i punti: P = (-1/3, 0) Q = (1,0) ® in cui è tangente all'asse x

Segno della derivata prima: f '(x) > 0 (crescente ) per (x < 0) È (x > 1)

Segno della derivata seconda: f '' (x) > 0 sempre (concavità rivolta verso l'alto)

Costruzione per fasi successive della funzione. Poiché la funzione presenta un asintoto obliquo ®

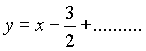
Poiché la funzione presenta un asintoto verticale (x = 0) e, come appare dal grafico:

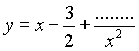
Inoltre, poiché

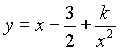
Il passaggio per il punto di coordinate (1,0) ci consente di determinare il valore di k = 1/2. Pertanto

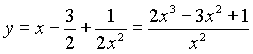
Torna a SCHEDA n.6