Sia f(x) un funzione continua in [a, b], si dice integrale definito della funzione e si indica con:

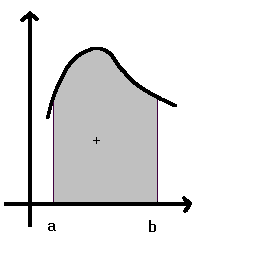
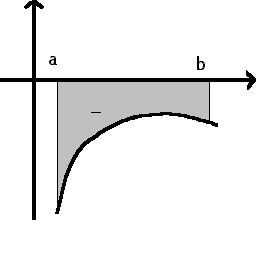
la differenza tra F(b) ed F(a), dove F(x) è la primitiva di f(x). L'integrale definito rappresenta la parte di piano racchiusa tra la curva e l'intervallo [a,b]. Se l'area sta sopra l'asse x è positiva, se sta sotto è negativa.

Graficamente si può avere:

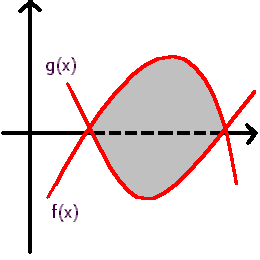
AREA LIMITATA DAL GRAFICO DI DUE FUNZIONI

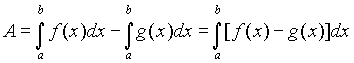
VOLUME DEI SOLIDI DI ROTAZIONE

Dati una funzione f(x) e un intervallo [a,b], il volume del solido generato da una rotazione completa della curva attorno all'asse delle x è dato da:

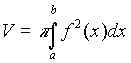
Dati una funzione g(y) e un intervallo [a,b], il volume del solido generato da una rotazione completa della curva attorno all'asse delle y è dato da:

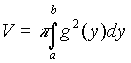
ESERCIZIO n.1

Dopo aver studiato la funzione y=x²e^x, calcolare l'area del dominio di piano delimitato dalla curva, dall'asse x e dalle rette x = -2 e x = 2

ESERCIZIO n.2

Considerata sul piano xOy la retta y = 3x -2 si calcoli il volume del solido generato dalla rotazione attorno all'asse x, relativa all'intervallo [-2,3]

Vai a SOLUZIONI

Torna all'ANGOLO DEI NUMERI