Un punto di ascissa x0 interno al dominio di una funzione f si dice di massimo relativo se:

esiste un intorno U di x0 tale che " x Î U risulti f(x) £ f(x0)

si dice di minimo relativo se esiste un intorno U di x0 tale che " x Î U risulti f(x) ³ f(x0)

Indica schematicamente un metodo per la ricerca di estremanti relativi:

Si calcola la derivata prima della funzione e si determinano i punti x0 (appartenenti al dominio) in cui f '(x0) = 0

Si studia il segno di f '(x) : se f '(x) > 0 a sinistra di x0 e f '(x) < 0 a destra di x0, allora f(x) ha un punto di massimo relativo in x0.

Un punto di ascissa x 0 interno al dominio di una funzione f si dice di flesso se:

in tale punto la funzione cambia concavità.

Indica schematicamente un metodo per la ricerca dei flessi:

Si calcola la derivata seconda della funzione e si determinano i punti x0 (appartenenti al dominio) in cui f ''(x0) = 0

Si studia il segno di f ''(x) : se f ''(x) > 0 a sinistra di x0 e f ''(x) < 0 a destra di x0, allora f(x) ha un punto di flesso in x0. Se risulta inoltre f '(x0) = 0 il flesso è a tangente orizzontale.

--------------------RISPOSTE agli ESERCIZI--------------------

ESERCIZIO n.1

Flessi a tangente obliqua :

x = 0

x = -3Ö 2

x = 3 Ö 2

Minimo relativo in x = - Ö 6

Massimo relativo in x = Ö 6

ESERCIZIO n.2

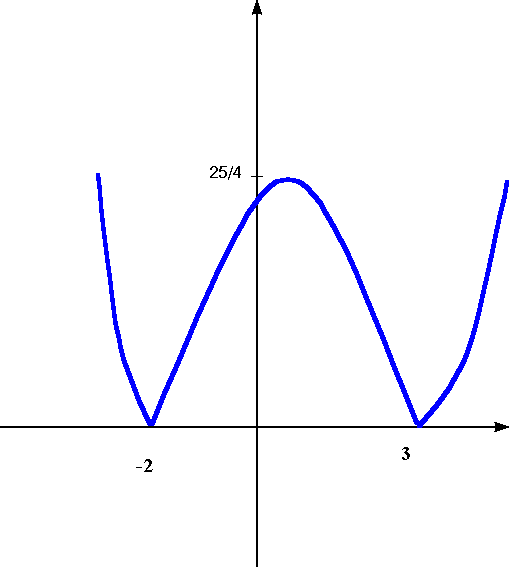
Il grafico della funzione è illustrato in figura. Nei punti di ascissa x = -2 e x = 3 la funzione non è derivabile e si annulla. Calcolando la derivata prima otteniamo:

f '(x) = 2x - 1 ® se x < -2

f '(x) = -2x + 1 ® se -2 £ x £ 3

f ' (x) = 2x - 1 ® se x > 3

Tale derivata consente di trovare l'unico massimo relativo in x = 1/2 . I punti in cui f non è derivabile sono dunque due punti di minimo.

Torna a SCHEDA n.8