LA GEOMETRIA IPERBOLICA
![]()
Il matematico tedesco FELIX KLEIN (1849-1925) ideò un modello di geometria iperbolica col quale mostrò che tale geometria soddisfa tutti gli assiomi della geometria euclidea, eccetto quello della parallele. Pertanto questo assioma è indipendente dai rimanenti e non può essere da essi dedotto.
KLEIN adottò come piano (iperbolico) la parte di piano delimitata da una circonferenza qualunque (o in generale da una conica qualunque), esclusi i punti di quest’ultima. Chiamò poi punti (iperbolici) i punti interni a tale cerchio, sempre esclusa la circonferenza, e infine chiamò retta (iperbolica) una corda di tale cerchio estremi esclusi. Un punto appartiene ad una retta quando punto e corda corrispondenti nel cerchio si appartengono.
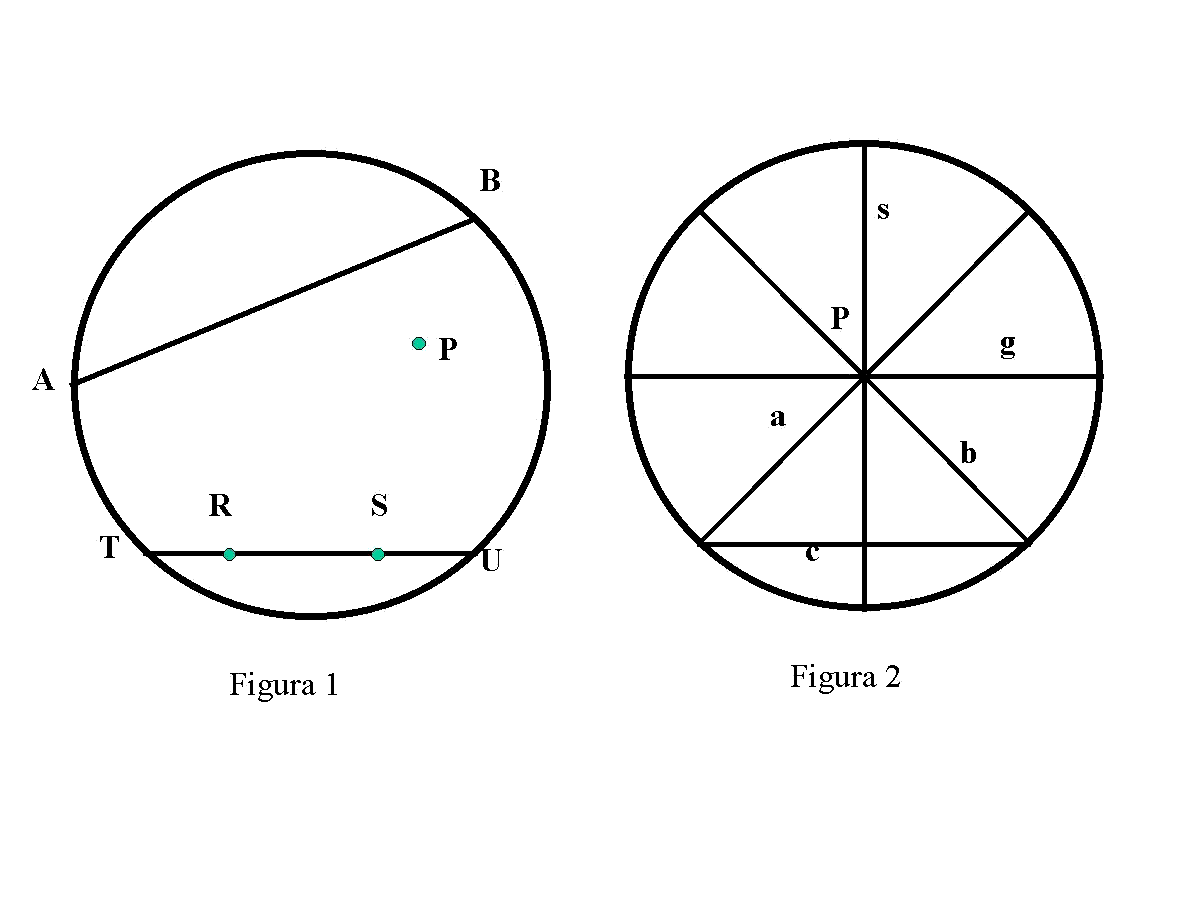
In figura 1, ad esempio, P è un punto iperbolico, mentre non lo sono A e B; AB è una retta iperbololica, inoltre RS, quale parte della retta TU, è un segmento.
In figura 2, se si considera il punto P, le due corde a e b passanti per P e per gli estremi della corda c sono le due parallele iperboliche che da P si possono condurre alla retta c.
Così tutte le rette (corde) passanti per P si dividono in due classi: le non secanti, come la g, dette anche iperparallele e le secanti come la s.
Si osservi in figura la definizione di semipiano, di angolo e di semiretta (che parte dal punto P).
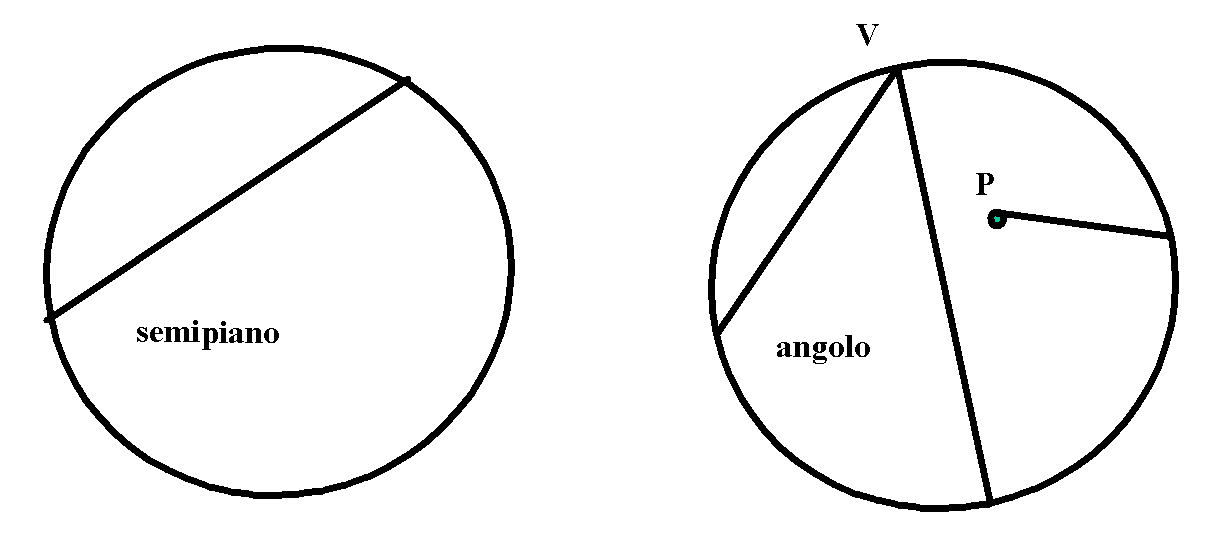
Si noti come l'assioma delle parallele, nel nostro piano non sia valido. Infatti, ammettendo la definizione di rette parallele come due rette complanari che non hanno alcun punto in comune, dato un punto P ed una retta r, da P alla retta r si possono condurre due parallele PA e PB.
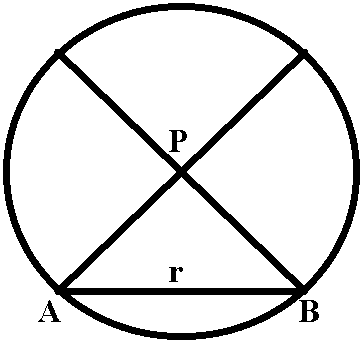
Si ricordi che A e B non sono ammissibili come punti perché stanno sulla circonferenza e che, perciò, l'affermazione che le due rette PA e PB non hanno punti in comune con la retta r è corretta.
![]()