Applicazione dei teoremi studiati
Quesito D proposto agli Esami di Stato 2002/2003
TESTO
Un aeromobile parte da A (lat.45° N; long. 008° E) e segue l'ortodromia definita
dalla rotta iniziale TC = 045°.
Un secondo aeromobile parte da B (lat. 45° N; long. 068° E) e segue l'ortodromia
definita dalla rotta iniziale TC=315°.
Il candidato calcoli le coordinate del punto di intersezione tra le due ortodromie.
Soluzione
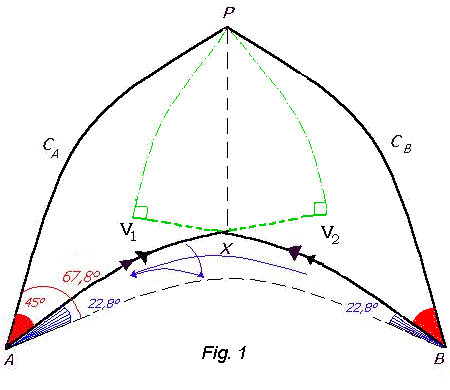
Costruiamo la scena:

|
L'angolo
|
è uguale a : |
360° - 315° = 45°
CA = CB = 45°
DlAB = 68° - 8° = 60°
Si applica il teorema di Eulero al triangolo sferico A-P-B per il calcolo della dAB :
cos dAB = cos CA cosCB + senCA senCB cosDl =
= cos 45° cos45° + sen45° sen45° cos60° = 0.75
dAB = arc cos 0.75 = 41.4° = 2484.57 NM (distanza ortodromica AB)
Si applica il teorema di Eulero al triangolo sferico A-P-B per il calcolo della rotta iniziale:
cosCB = cos CA cos dAB + senCA sen dAB cos Ri
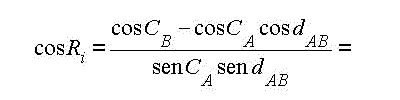

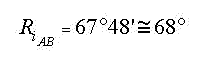 |
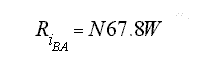 |
|
Operazioni sul triangolo sferico A
- X - B
|
|
L'angolo
|
è uguale all'angolo
|
(= 67.8° - 45°) = 22.8°.
|
Si applica la regola di Vieta al triangolo sferico A-X-B per il calcolo della dAX :
( N. B. Si sarebbe potuto applicare indifferentemente il teorema di Eulero)
cotg dAX sen 41.4° = cos 41.4°cos22.8° + sen22.8° cotg22.8°
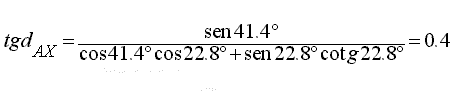
dAX = arctg 0.4 = 22° 17' = 1337.3 NM
|
Operazioni sul triangolo sferico
P- A - X
|
Si applica il teorema di Eulero per il calcolo di CX :
cos CX = cosCA cos dAX + senCA sen dAX cos45° =
= cos45°cos22.17°+ sen45°sen22.17°cos45° = 0.84
CX = arc cos 0.84 = 32.44° = 32° 27'
Si calcola, a questo punto, jX , latitudine del punto d'incontro:
jX = 90° - CX = 57° 33' N
Si applica ora il teorema di Eulero per il calcolo di DlAX.
cos dAX =cosCA cosCX + senCA senCXcosDlAX
|
cosDlAX
=
|
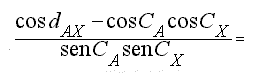 |
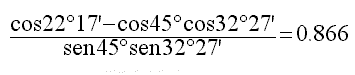
DlAX = arc cos 0.866 = 80° E
lX =lA + 30° = 38° (longitudine del punto d'incontro)
In definitiva X = ( 57° 33' N ; 38° E )
Concludiamo spendendo due parole sul calcolo dei vertici delle due ortodromie, benchè non sia richiesto esplicitamente dal problema. Come si evince dalla fig. 1), i vertici delle due ortodromie stanno alla stessa latitudine (j = 60° N ) ma a longitudini diverse, precisamente:
cotg DlAV1 = senjA tg Ri = sen 45° tg 45°
| DlAV1 = 54° 44' E | lV1 = 8°+54°44' = 62°44' E |
mentre:
| cotg DlBV2 = - sen 45° | DlBV2 = 54°44' W | lV2 =68° - 54°44' = 13°16' E |
Invece le latitudini dei vertici V1 e V2 coincidono, infatti, essendo:
cosjV = cosj senRi
ed avendo j ed Ri gli stessi valori nei punti A e B, segue che: jV1= jV2= 60°
|
Torna ai quesiti del 2003
|